建模#

简介#

MuJoCo 可以加载其原生 MJCF 格式的 XML 模型文件，也可以加载流行但功能更受限的 URDF 格式。本章是 MJCF 建模指南。参考手册可在 XML 参考章节中找到。URDF 的文档可以在其他地方找到；这里我们只描述 MuJoCo 特有的 URDF 扩展。

MJCF 模型可以表示具有广泛特性和模型元素的复杂动力学系统。要访问所有这些特性，需要一种丰富的建模格式，如果设计时不考虑可用性，这种格式可能会变得很繁琐。因此，我们努力将 MJCF 设计成一种可扩展的格式，允许用户从小处着手，之后再构建更详细的模型。在这方面特别有帮助的是受 HTML 中内联级联样式表 (CSS) 思想启发的广泛的默认设置机制。它使用户能够快速创建新模型并进行实验。实验过程还得到了众多选项的辅助，这些选项可用于重新配置仿真流程；此外，快速重新加载功能使得模型编辑成为一个交互式过程。

我们可以将 MJCF 视为一种建模格式和一种编程语言的混合体。它有一个内置的编译器，这通常是与编程语言相关的概念。虽然 MJCF 没有通用编程语言的强大功能，但根据模型的设计方式，会自动调用许多复杂的编译时计算。

加载模型#

正如在“概述”章节的模型实例中所解释的，MuJoCo 模型可以从 MJCF 或 URDF 格式的纯文本 XML 文件中加载，然后编译成一个低级的 mjModel。或者，可以从二进制 MJB 文件中直接加载先前保存的 mjModel——其格式未被文档化，但本质上是 mjModel 内存缓冲区的副本。MJCF 和 URDF 文件使用 mj_loadXML 加载，而 MJB 文件使用 mj_loadModel 加载。

加载 XML 文件时，它首先被内部使用 TinyXML 解析器解析成文档对象模型 (DOM)。然后，此 DOM 被处理并转换为一个高级的 mjSpec 对象。转换取决于模型格式——这是从 XML 文件中的顶级元素推断出来的，而不是从文件扩展名。回想一下，一个有效的 XML 文件有一个唯一的顶级元素。对于 MJCF，此元素必须是 mujoco，对于 URDF，必须是 robot。

编译模型#

一旦创建了一个高级的 mjSpec——通过加载 MJCF 文件或 URDF 文件，或以编程方式——它就会被编译成 mjModel。编译与加载无关，这意味着无论 mjSpec 是如何创建的，编译器都以相同的方式工作。解析器和编译器都执行广泛的错误检查，并在遇到第一个错误时中止。由此产生的错误消息包含 XML 文件中的行号和列号，并且是自解释的，因此我们不在这里记录它们。解析器使用自定义模式来确保文件结构、元素和属性有效。然后，编译器应用许多额外的语义检查。最后，对编译后的模型执行一个仿真步骤，并拦截任何运行时错误。后者是通过（临时）将 mju_user_error 指向一个抛出 C++ 异常的函数来完成的；如果需要，用户可以在运行时实现类似的错误拦截功能。

整个解析和编译过程非常快——如果模型不包含需要通过仿真计算的大型网格或执行器长度范围，则不到一秒。这使得以交互方式设计模型成为可能，通过频繁重新加载并可视化更改。请注意，simulate.cc 代码示例有一个用于重新加载当前模型的键盘快捷键 (Ctrl+L)。

保存模型#

一个 MJCF 模型可以由多个（包含的）XML 文件以及从 XML 中引用的网格、高度场和纹理组成。编译后，所有这些文件的内容都被组装到 mjModel 中，可以使用 mj_saveModel 将其保存为二进制 MJB 文件。MJB 是一个独立的文件，不引用任何其他文件。它的加载速度也更快。因此，我们建议将常用模型保存为 MJB，并在需要仿真时加载它们。

也可以使用 mj_saveLastXML 将编译后的 mjSpec 保存为 MJCF。如果在编译后相应的 mjModel 中的任何实值字段被修改（这不常见，但可能发生在系统辨识应用中），这些修改会在保存前自动复制回 mjSpec。请注意，编译后的模型不能进行结构性更改。XML 写入器试图生成最小的 MJCF 文件，该文件保证能编译成相同的模型，除了由实值的纯文本表示引起的微不足道的数值差异。生成的文件可能与原始文件结构不同，因为 MJCF 有许多方便用户的功能，允许以不同方式指定相同的模型。XML 写入器使用 MJCF 的一个“规范”子集，其中所有坐标都是局部的，所有物体的姿态、方向和惯性属性都明确指定。在“计算”章节中，我们展示了一个示例 MJCF 文件和相应的已保存示例。

编辑模型#

从 MuJoCo 3.2 开始，可以使用 mjSpec 结构体及相关 API 创建和修改模型。有关更多文档，请参阅模型编辑章节。

MJCF 机制#

MJCF 使用几种跨越多个模型元素的机制来创建模型。为避免重复，我们仅在本节中详细描述它们。这些机制不对应于“计算”章节中介绍的仿真概念之外的新概念。它们的作用是简化 MJCF 模型的创建，并能够在不需要手动转换为规范格式的情况下使用不同的数据格式。

运动学树#

MJCF 文件的主要部分是由嵌套的 body 元素创建的 XML 树。顶层物体是特殊的，称为 worldbody。这种树状组织与 URDF 形成对比，URDF 是先创建一组连杆，然后用指定子连杆和父连杆的关节将它们连接起来。在 MJCF 中，子物体在 XML 意义上确实是父物体的子元素。

当在物体内部定义一个关节时，它的功能不是连接父子物体，而是在它们之间创建运动自由度。如果在给定的物体内没有定义关节，那么该物体就焊接在其父物体上。MJCF 中的一个物体可以包含多个关节，因此不需要引入虚拟物体来创建复合关节。相反，只需在同一个物体内定义所有构成所需复合关节的基本关节。例如，两个滑块和一个铰链可以用来模拟一个在平面上运动的物体。

其他 MJCF 元素可以在由嵌套物体元素创建的树中定义，特别是关节 (joint)、几何体 (geom)、站点 (site)、相机 (camera)、灯光 (light)。当一个元素在物体内定义时，它固定在该物体的局部坐标系中，并始终随其移动。引用多个物体或根本不引用物体的元素在运动学树之外的单独部分中定义。

默认设置#

MJCF 有一个精巧的机制用于设置默认属性值。这使我们能够在拥有大量元素和属性以展现软件丰富功能的同时，编写简短且可读的模型文件。该机制还允许用户在一处进行更改，并让其在整个模型中传播。我们从一个例子开始。

<mujoco>
  <default class="main">
    <geom rgba="1 0 0 1"/>
    <default class="sub">
      <geom rgba="0 1 0 1"/>
    </default>
  </default>

  <worldbody>
    <geom type="box"/>
    <body childclass="sub">
      <geom type="ellipsoid"/>
      <geom type="sphere" rgba="0 0 1 1"/>
      <geom type="cylinder" class="main"/>
    </body>
  </worldbody>
</mujoco>

这个例子实际上无法编译，因为缺少一些必需信息，但在这里我们只关心 geom 的 rgba 值的设置。上面创建的四个 geom 最终会因为默认设置机制而得到以下 rgba 值

几何体类型	几何体 rgba
长方体 (box)	1 0 0 1
椭球体 (ellipsoid)	0 1 0 1
球体 (sphere)	0 0 1 1
圆柱体 (cylinder)	1 0 0 1

长方体使用顶层默认类“main”来设置其未定义属性的值，因为没有指定其他类。物体指定了子类“sub”，导致该物体的所有子元素（以及它们的所有子元素等）都使用类“sub”，除非另有指定。因此，椭球体使用类“sub”。球体明确定义了 rgba，这覆盖了默认设置。圆柱体指定了默认类“main”，因此它使用“main”而不是“sub”，即使后者在包含该 geom 的物体的 childclass 属性中指定了。

现在我们描述一般规则。MuJoCo 支持无限数量的默认类，这些类由 XML 中可能嵌套的 default 元素创建。每个类都有一个唯一的名称——这是一个必需的属性，但顶层类的名称如果未定义则为“main”。每个类还包含一套完整的虚拟模型元素，其属性设置如下。当一个默认类在另一个默认类中定义时，子类自动继承父类的所有属性值。然后它可以通过定义相应的属性来覆盖部分或全部属性值。顶层默认类没有父类，因此其属性被初始化为内部默认值，这些默认值显示在参考章节中。

默认类中包含的虚拟元素不是模型的一部分；它们仅用于初始化实际模型元素的属性值。当一个实际元素首次创建时，其所有属性都从当前活动的默认类中相应的虚拟元素复制而来。总会有一个活动的默认类，可以通过以下三种方式之一确定。如果当前元素或其任何祖先物体中没有指定类，则使用顶层类（无论它被称为“main”还是其他名称）。如果当前元素没有指定类，但其一个或多个祖先物体指定了 childclass，则使用最近的祖先物体的 childclass。如果当前元素指定了一个类，则使用该类，而忽略其祖先物体中的任何 childclass 属性。

一些属性，如物体惯性，可以处于一种特殊的未定义状态。这指示编译器从其他信息中推断相应的值，在这种情况下是附着在物体上的几何体的惯性。未定义状态不能在 XML 文件中输入。因此，一旦一个属性在给定的类中被定义，它就不能在该类或其任何子类中被取消定义。所以，如果目标是在给定的模型元素中将某个属性保留为未定义，那么它在活动的默认类中也必须是未定义的。

这里最后一个复杂之处是执行器。它们是不同的，因为一些与执行器相关的元素实际上是快捷方式，而快捷方式与默认设置机制的交互方式并不直观。这在下面的执行器快捷方式部分中解释。

坐标系#

在运动学树中定义的所有元素的位置和方向都以局部坐标表示，对于物体是相对于其父物体，对于几何体、关节、站点、相机和灯光则是相对于包含该元素的物体。

一个相关的属性是 compiler/angle。它指定 MJCF 文件中的角度是以度还是弧度表示（编译后，角度总是以弧度表示）。

位置使用以下方式指定

pos: real(3), “0 0 0”: 相对于父物体的位置。

坐标系方向#

几个模型元素都关联有右手空间坐标系。这些是运动学树中除关节外的所有定义元素。空间坐标系由其位置和方向定义。指定 3D 位置是直接的，但指定 3D 方向可能具有挑战性。这就是为什么 MJCF 提供了几种替代机制。无论用户选择哪种机制，坐标系方向在内部总是被转换为单位四元数。回想一下，围绕单位向量 \((x, y, z)\) 旋转角度 \(a\) 的 3D 旋转对应于四元数 \((\cos(a/2), \: \sin(a/2) \cdot (x, y, z))\)。还要回想一下，每个 3D 方向都可以通过围绕某个轴旋转某个角度的单个 3D 旋转来唯一指定。

所有具有空间坐标系的 MJCF 元素都允许下面列出的五个属性。坐标系方向最多使用这些属性中的一个来指定。quat 属性有一个对应于零旋转的默认值，而其他属性则被初始化为特殊的未定义状态。因此，如果用户没有指定这些属性中的任何一个，坐标系就不会被旋转。

quat: real(4), “1 0 0 0”: 如果四元数已知，这是指定坐标系方向的首选方式，因为它不涉及转换。相反，它在编译期间被归一化为单位长度并复制到 mjModel 中。当模型保存为 MJCF 时，所有坐标系方向都使用此属性以四元数表示。
axisangle: real(4), optional: 这些是上面提到的量 \((x, y, z, a)\)。最后一个数字是旋转角度，单位为度或弧度，由 compiler 的 angle 属性指定。前三个数字确定一个 3D 向量，即旋转轴。该向量在编译期间被归一化为单位长度，因此用户可以指定任意非零长度的向量。请记住，旋转是右旋的；如果向量 \((x, y, z)\) 的方向反转，将导致相反的旋转。改变 \(a\) 的符号也可以用来指定相反的旋转。
euler: real(3), optional: 围绕三个坐标轴的旋转角度。应用这些旋转的轴序列由 compiler 的 eulerseq 属性确定，并且对整个模型都是相同的。
xyaxes: real(6), optional: 前 3 个数字是坐标系的 X 轴。后 3 个数字是坐标系的 Y 轴，它会自动与 X 轴正交。然后 Z 轴被定义为 X 轴和 Y 轴的叉积。
zaxis: real(3), optional: 坐标系的 Z 轴。编译器找到将向量 \((0, 0, 1)\) 映射到此处指定的向量的最小旋转。这隐式地确定了坐标系的 X 轴和 Y 轴。这对于围绕 Z 轴具有旋转对称性的几何体以及灯光（它们沿其坐标系的 Z 轴定向）很有用。

求解器参数#

“计算”章节的求解器参数部分解释了决定 MuJoCo 中约束行为的量 \(d, b, k\) 的数学和算法意义。在这里，我们解释如何设置它们。设置是间接完成的，通过在所有涉及约束的 MJCF 元素中可用的属性 solref 和 solimp。这些参数可以按每个约束、每个默认类进行调整，或者保持未定义——在这种情况下，MuJoCo 使用下面显示的内部默认值。另请注意 option 中可用的覆盖机制；它可用于在运行时更改所有与接触相关的求解器参数，以便交互式地试验参数设置或实现用于数值优化的连续方法。

在这里，我们关注单个标量约束。使用与“计算”章节略有不同的符号，让 \(\ac\) 表示加速度，\(v\) 表示速度，\(r\) 表示位置或残差（在摩擦维度中定义为 0），\(k\) 和 \(b\) 表示用于定义参考加速度 \(\ar = -b v - k r\) 的虚拟弹簧的刚度和阻尼。让 \(d\) 表示约束阻抗，\(\au\) 表示没有约束力时的加速度。我们早先的分析揭示了约束空间中的动力学近似为

(1)#\[\ac + d \cdot (b v + k r) = (1 - d)\cdot \au \]

同样，用户可以控制的参数是 \(d, b, k\)。其余的量是系统状态的函数，并在每个时间步自动计算。

阻抗#

我们首先解释约束阻抗 \(d\)。

阻抗的直观描述

阻抗 \(d \in (0, 1)\) 对应于约束产生力的能力。小的 \(d\) 值对应于弱约束，而大的 \(d\) 值对应于强约束。阻抗在任何时候都影响约束，特别是在系统处于静止状态时。阻抗使用 solimp 属性设置。

回想一下，\(d\) 必须介于 0 和 1 之间；在内部，MuJoCo 将其钳位在 [mjMINIMP mjMAXIMP] 范围内，目前设置为 [0.0001 0.9999]。它使求解器在无力加速度 \(\au\) 和参考加速度 \(\ar\) 之间进行插值。用户可以将 \(d\) 设置为常数，或者利用其插值特性使其与位置相关，即作为约束违规 \(r\) 的函数。与位置相关的阻抗可用于模拟物体周围的软接触层，或定义随着违规增大而变强的等式约束（例如，为了近似齿隙）。函数 \(d(r)\) 的形状由特定于元素的参数向量 solimp 决定。

solimp : real(5), “0.9 0.95 0.001 0.5 2”

这五个数字 (\(d_0\), \(d_\text{width}\), \(\text{width}\), \(\text{midpoint}\), \(\text{power}\)) 参数化了 \(d(r)\) —— 阻抗 \(d\) 作为约束违规 \(r\) 的函数。

前 3 个值表示当 \(r\) 从 \(0\) 变化到 \(\text{width}\) 时，阻抗将平滑变化

\[d(0) = d_0, \quad d(\text{width}) = d_\text{width} \]

第 4 和第 5 个值，\(\text{midpoint}\) 和 \(\text{power}\)，控制在 \(d_0\) 和 \(d_\text{width}\) 之间插值的 S 形函数的形状，如下方图表所示。图表显示了两个反射的 S 形曲线，因为阻抗 \(d(r)\) 取决于 \(r\) 的绝对值。\(\text{power}\)（用于生成函数的多项式样条的幂）必须为 1 或更大。\(\text{midpoint}\)（指定拐点）必须在 0 和 1 之间，并以 \(\text{width}\) 为单位表示。请注意，当 \(\text{power}\) 为 1 时，无论 \(\text{midpoint}\) 为何值，函数都是线性的。

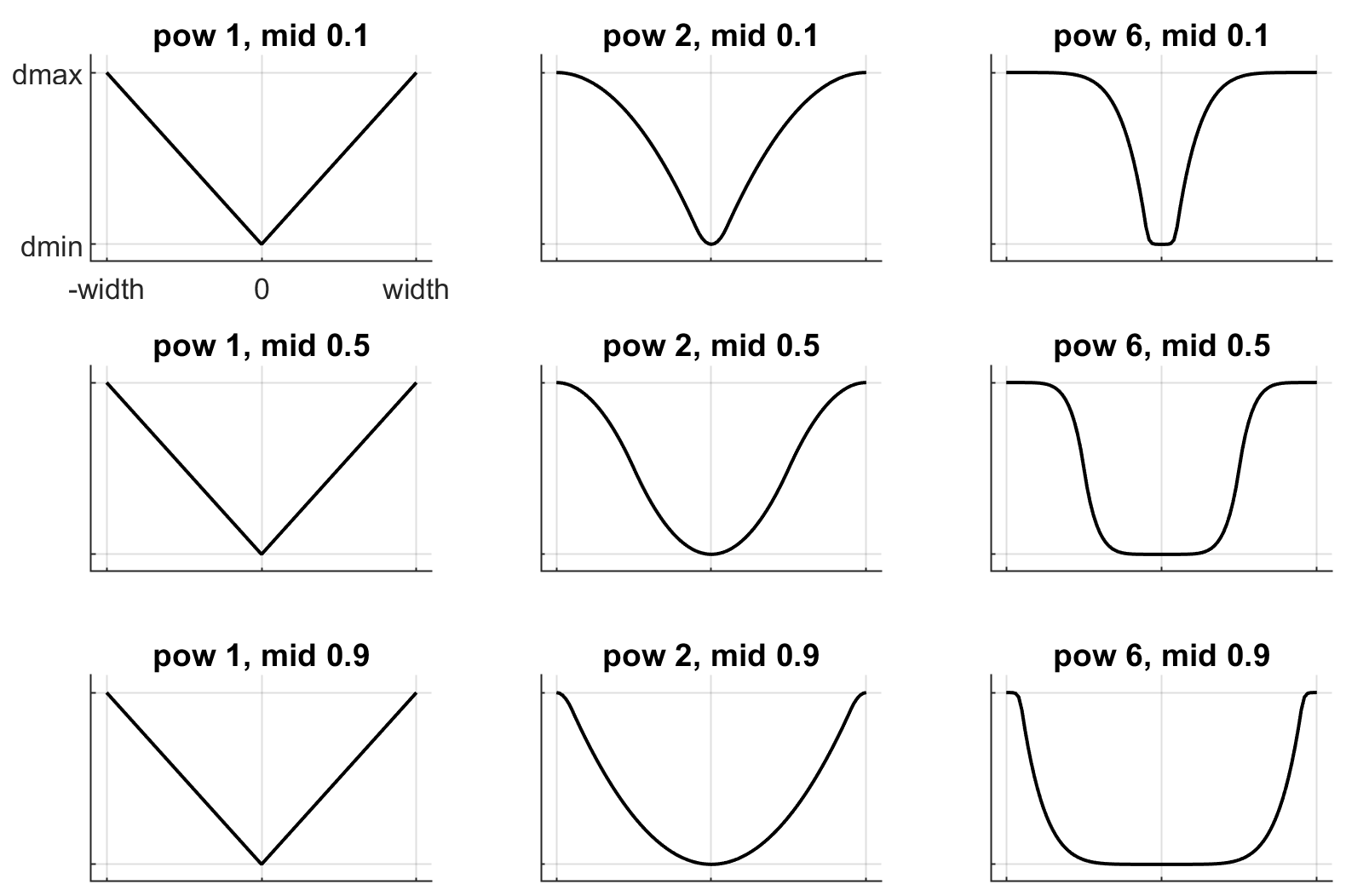
这些图表显示了垂直轴上的阻抗 \(d(r)\)，作为水平轴上约束违规 \(r\) 的函数。

对于等式约束，\(r\) 是约束违规。对于限制、椭圆锥的法线方向和金字塔锥的所有方向，\(r\) 是（限制或接触）距离减去约束变为活动状态的边距；对于接触，此边距是 margin-gap。当 \(r < 0\)（穿透）时，限制和接触约束是活动的。

对于摩擦损失或椭圆锥的摩擦维度，违规 \(r\) 恒为零，因此只有 \(d(0)\) 影响这些约束，所有其他 solimp 值都被忽略。

平滑性和可微性

对于完全平滑（可微）的动力学，限制和接触应具有 \(d_0=0\) (solimp[0]=0)。特别是对于接触，应牢记与 geom 相关的求解器参数的混合规则。另请参阅计算章节中和 mjd_transitionFD 文档中关于导数的讨论。

参考#

接下来我们解释控制参考加速度 \(\ar\) 的刚度 \(k\) 和阻尼 \(b\) 的设置。

参考加速度的直观描述

参考加速度 \(\ar\) 决定了约束为纠正违规而试图实现的运动。想象一个物体掉落到平面上。撞击时，约束将产生一个法向力，试图用特定的运动来纠正穿透；这个运动就是参考加速度。

另一种理解参考加速度的方法是考虑在计算章节中描述的未建模的变形变量。想象两个物体被压在一起，导致接触处发生变形。现在非常快地将这两个物体拉开；变形在恢复到未变形状态时所发生的运动就是参考加速度。

这个加速度由两个数字定义，一个刚度 \(k\) 和一个阻尼 \(b\)，可以直接设置，也可以重新参数化为质量-弹簧-阻尼系统（一个谐振子）的时间常数和阻尼比。参考加速度由 solref 属性控制。

此属性有两种格式，由数字的符号决定。如果两个数字都是正数，则该规范被认为是 \((\text{timeconst}, \text{dampratio})\) 格式。如果是负数，则是“直接”的 \((-\text{stiffness}, -\text{damping})\) 格式。

残差恒为 0 的摩擦约束具有一阶动力学，下面的质量-弹簧-阻尼分析不适用。在这种情况下，时间常数是约束速度的指数衰减率，阻尼比被忽略。等效地，在直接格式中，\(\text{stiffness}\) 被忽略。

solref : real(2), “0.02 1”

我们首先描述默认的正值格式，其中两个数字是 \((\text{timeconst}, \text{dampratio})\)。

这里的想法是根据质量-弹簧-阻尼系统的时间常数和阻尼比来重新参数化模型。我们所说的“时间常数”是指自然频率的倒数乘以阻尼比。在这种情况下，我们使用质量-弹簧-阻尼模型，在经过适当缩放后计算 \(k, b\)。请注意，有效刚度 \(d(r) \cdot k\) 和阻尼 \(d(r) \cdot b\) 会被阻抗 \(d(r)\) 缩放，而阻抗是距离 \(r\) 的函数。因此，我们不能总是实现指定的质量-弹簧-阻尼特性，除非我们完全撤销 \(d\) 的缩放。但后者是不可取的，因为它会破坏插值属性，特别是 \(d=0\) 的极限将不再禁用约束。相反，我们缩放刚度和阻尼，使阻尼比保持不变，而当 \(d(r)\) 变小时，时间常数增加。缩放公式为

\[\begin{aligned} b &= 2 / (d_\text{width}\cdot \text{timeconst}) \\ k &= d(r) / (d_\text{width}^2 \cdot \text{timeconst}^2 \cdot \text{dampratio}^2) \\ \end{aligned} \]

timeconst 参数应至少比仿真时间步长大两倍，否则系统相对于数值积分器可能会变得过于刚硬（尤其是在使用欧拉积分时），并且仿真可能会变得不稳定。除非将 flag 的 refsafe 属性设置为 false，否则这将在内部强制执行。\(\text{dampratio}\) 参数通常会设置为 1，对应于临界阻尼。较小的值会导致欠阻尼或有弹性的约束，而较大的值会导致过阻尼约束。将上述公式与 (1) 结合，我们可以推导出以下结果。如果参考加速度使用正数格式给出，并且阻抗是常数 \(d = d_0 = d_\text{width}\)，则静止时的穿透深度为

\[r = \au \cdot (1 - d) \cdot \text{timeconst}^2 \cdot \text{dampratio}^2 \]

接下来，我们描述直接格式，其中两个数字是 \((-\text{stiffness}, -\text{damping})\)。这尤其允许直接控制恢复系数。我们仍然应用一些缩放，以便相同的数字可以用于不同的阻抗，但缩放不再依赖于 \(r\)，并且这两个数字不再相互作用。缩放公式为

\[\begin{aligned} b &= \text{damping} / d_\text{width} \\ k &= \text{stiffness} \cdot d(r) / d_\text{width}^2 \\ \end{aligned} \]

与上述推导类似，如果参考加速度使用负数格式给出且阻抗为常数，则静止时的穿透深度为

\[r = \frac{\au (1 - d)}{\text{stiffness}} \]

提示

在正值默认格式中，\(\text{timeconst}\) 参数控制约束的柔软度。它以时间单位指定，意思是“约束试图多快解决违规”。较大的值对应于较软的约束。

负值的“直接”格式更灵活，例如允许完全弹性碰撞 (\(\text{damping} = 0\))。它是系统辨识的推荐格式。

在正值格式中，\(\text{dampratio}\) 为 1 等效于在直接格式中 \(\text{damping} = 2 \sqrt{ \text{stiffness} }\)。

接触参数#

每个接触的参数在“计算”章节的接触部分中已描述。这里我们解释如何设置这些参数。如果几何体对由 XML 元素 pair 显式定义，它具有直接指定所有接触参数的属性。在这种情况下，单个几何体的参数被忽略。另一方面，如果接触是由动态机制生成的，则其参数需要从接触对中的两个几何体推断。如果两个几何体具有相同的参数，则无需任何操作，但如果它们的参数不同怎么办？在这种情况下，我们使用几何体属性 solmix 和 priority 来决定如何组合它们。每个接触参数的组合规则如下

condim

如果两个几何体中的一个具有更高的优先级，则使用其 condim。如果两个几何体具有相同的优先级，则使用两个 condim 中的最大值。这样，一个无摩擦的几何体和一个有摩擦的几何体形成一个有摩擦的接触，除非无摩擦的几何体具有更高的优先级。后者在粒子系统中是可取的，例如，我们可能不希望粒子粘附到任何物体上。

friction

回想一下，接触最多可以有 5 个摩擦系数：两个切向，一个扭转，两个滚动。mjData.contact 中的每个接触实际上都有所有 5 个，即使 condim 小于 6 并且并非所有系数都被使用。相比之下，几何体只有 3 个摩擦系数：切向（两个轴相同），扭转，滚动（两个轴相同）。每个这样的 3D 摩擦系数向量通过复制切向和滚动分量扩展为 5D 摩擦系数向量。关于切向、扭转和滚动系数的语义的直观描述，请参阅“计算”章节中的接触部分。

接触摩擦系数随后根据以下规则计算：如果两个几何体中的一个具有更高的优先级，则使用其摩擦系数。否则，使用两个几何体上每个摩擦系数的逐元素最大值。

每个接触有 5 个系数而每个几何体只有 3 个的原因如下。对于一个接触对，我们希望允许我们的求解器能够处理的最灵活的模型。如前所述，各向异性摩擦可以用来模拟滑冰等效果。但这需要知道接触切平面的两个轴是如何定向的。对于一个预定义的接触对，我们预先知道两个几何体的类型，并且相应的碰撞函数总是以相同的方式生成接触坐标系——我们在这里不描述它，但可以在可视化器中看到。然而，对于单个几何体，我们不知道它们可能会与哪些其他几何体碰撞以及它们的几何体类型可能是什么，因此在指定单个几何体时无法知道接触切平面将如何定向。这就是为什么 MuJoCo 不允许在单个几何体规范中使用各向异性摩擦，而只在显式接触对规范中允许。

margin, gap

使用两个几何体边距（或间隙）的最大值。这里忽略了几何体优先级，因为边距和间隙是距离属性，单边指定没有多大意义。

solref, solimp: 如果两个几何体中的一个具有更高的优先级，则使用其 solref 和 solimp 参数。如果两个几何体具有相同的优先级，则使用加权平均值。权重与 solmix 属性成正比，即 weight1 = solmix1 / (solmix1 + solmix2)，weight2 类似。此加权平均规则有一个重要的例外。如果任一几何体的 solref 为非正数，即它依赖于直接格式，则无论 solmix 如何，都使用逐元素最小值。这是因为对不同格式的 solref 参数进行平均将是无意义的。

接触覆盖#

MuJoCo 使用了一个在“计算”章节中描述的复杂且新颖的约束模型。要对这个模型的工作原理获得直观理解，需要进行一些实验。为了方便这个过程，我们提供了一种机制来覆盖一些求解器参数，而无需对实际模型进行更改。一旦禁用覆盖，仿真将恢复到模型中指定的参数。这种机制也可以用于在数值优化（如最优控制或状态估计）的背景下实现连续方法。这是通过允许接触在优化的早期阶段从远处起作用——以帮助优化器找到梯度并接近一个好的解决方案——然后在后期减少这种效应，使最终解决方案在物理上更现实。

这里的相关设置是 flag 的 override 属性，它启用和禁用此机制，以及 option 的 o_margin、o_solref、o_solimp 属性，它们指定新的求解器参数。请注意，覆盖仅适用于接触，而不适用于其他类型的约束。原则上，MuJoCo 模型中有许多实值参数可以从类似的覆盖机制中受益。然而，我们必须在某个地方划清界限，而接触是自然的选择，因为它们产生了最丰富但最难调整的行为。此外，接触动力学通常在数值优化方面构成挑战，经验表明，对接触参数进行连续化可以帮助避免局部最小值。

用户参数#

一些 MJCF 元素具有可选属性 user，它定义了一个自定义的、特定于元素的参数数组。这与 size 元素的相应“nuser_XXX”属性相互作用。例如，如果我们将 nuser_geom 设置为 5，那么 mjModel 中的每个几何体都将有一个包含 5 个实值参数的自定义数组。这些特定于几何体的参数要么在 MJCF 文件中通过 geom 的 user 属性定义，要么如果省略此属性，则由编译器设置为 0。所有“nuser_XXX”属性的默认值为 -1，这指示编译器自动将此值设置为模型中定义的最大关联 user 属性的长度。MuJoCo 不在任何内部计算中使用这些参数；相反，它们可用于自定义计算。解析器允许 XML 中任意长度的数组，编译器稍后将它们调整为 nuser_XXX 的长度。

一些通常用于内部计算的特定于元素的参数也可以用于自定义计算。这是通过安装覆盖仿真流程部分的用户回调来完成的。例如，通用执行器元素具有属性 dyntype 和 dynprm。如果 dyntype 设置为“user”，那么 MuJoCo 将调用 mjcb_act_dyn 来计算执行器动力学，而不是调用其内部函数。由 mjcb_act_dyn 指向的用户函数可以按其希望的任何方式解释在 dynprm 中定义的参数。但是，此参数数组的长度不能更改（与前面描述的自定义数组不同，其长度在 MJCF 文件中定义）。这同样适用于其他回调。

除了上面描述的特定于元素的用户参数外，还可以通过 custom 元素在模型中包含全局数据。对于在仿真过程中发生变化的数据，还有数组 mjData.userdata，其大小由 size 元素的 nuserdata 属性决定。

求解器设置#

约束力和受约束加速度的计算涉及数值求解一个优化问题。MuJoCo 有三种算法来解决这个优化问题：CG、Newton、PGS。它们中的每一种都可以应用于金字塔形或椭圆形摩擦锥模型，并使用密集或稀疏的约束雅可比矩阵。此外，用户可以指定最大迭代次数和控制提前终止的容差水平。还有一个第二 Noslip 求解器，这是一个后处理步骤，通过指定一个正的 noslip 迭代次数来启用。所有这些算法设置都可以在 option 元素中指定。

默认设置对大多数模型都适用，但在某些情况下需要调整算法。最好的方法是试验相关设置，并使用 simulate.cc 中的可视化分析器，它显示了不同计算的计时以及每次迭代的求解器统计信息。我们可以提供以下一般性指导和观察

对于小模型，约束雅可比矩阵应为稠密；对于大模型，应为稀疏。默认设置为“auto”；当自由度数量最多为 60 时，它解析为稠密，超过 60 时则为稀疏。但请注意，阈值最好根据活动约束的数量来定义，这取决于模型和行为。
在金字塔形和椭圆形摩擦锥之间的选择更多是建模选择而非算法选择，即它会导致用相同算法解决的不同优化问题。椭圆形摩擦锥更接近物理现实。然而，金字塔形摩擦锥可以提高算法的性能——但并非总是如此。虽然默认是金字塔形，但我们建议尝试椭圆形摩擦锥。当接触滑移是个问题时，抑制它的最好方法是使用椭圆形摩擦锥、大的 impratio 和具有非常小容差的牛顿算法。如果这还不够，请启用 Noslip 求解器。
牛顿算法是大多数模型的最佳选择。它在全局最小值附近具有二次收敛性，并且在惊人少的迭代次数内达到——通常在 5 次左右，很少超过 20 次。它应该与激进的容差值一起使用，比如 1e-10，因为它能够在不增加延迟的情况下实现高精度（由于末端的二次收敛）。我们看到它变慢的唯一情况是具有椭圆形摩擦锥和许多滑动接触的大型模型。在该情况下，海森矩阵分解需要大量更新。在一些大型模型中，由于模型元素的不幸排序导致高填充度（计算最优消元顺序是 NP 难的，所以我们依赖于启发式方法），它也可能变慢。请注意，可以在分析器中监控分解后的海森矩阵中的非零元素数量。
CG 算法在上述牛顿算法变慢的情况下表现良好。总的来说，CG 表现出具有良好速率的线性收敛，但在迭代次数方面无法与牛顿算法竞争，尤其是在需要高精度时。然而，它的迭代速度要快得多，并且不受填充或椭圆锥增加的复杂性影响。如果牛顿算法被证明太慢，请尝试 CG。
PGS 求解器在自由度数量大于约束数量时是最佳选择。PGS 解决一个约束优化问题，根据我们的经验，它具有次线性收敛性，但通常在前几次迭代中取得快速进展。因此，当可以容忍不精确的解时，它是一个不错的选择。对于具有大质量比或导致条件不良的其他模型属性的系统，PGS 的收敛速度往往相当慢。请记住，PGS 执行顺序更新，因此在物理上应该对称的系统中会破坏对称性。相比之下，CG 和牛顿算法执行并行更新并保持对称性。
Noslip 求解器是一个修改过的 PGS 求解器。它作为主求解器（可以是 Newton、CG 或 PGS）之后的后处理步骤执行。主求解器更新所有未知数。相比之下，Noslip 求解器只更新摩擦维度中的约束力，并忽略约束正则化。这具有抑制由软约束模型引起的漂移或滑移的效果。然而，这种优化步骤的级联不再解决一个明确定义的优化问题（或任何其他问题）；相反，它只是一个临时的机制。虽然它通常能完成任务，但我们在具有更复杂的多重接触相互作用的模型中看到了一些不稳定性。
PGS 在计算约束空间中的逆惯量方面有设置成本（就 CPU 时间而言）。类似地，牛顿算法对于海森矩阵的初始分解有设置成本，并根据之后需要多少次分解更新而产生额外的分解成本。CG 没有任何设置成本。由于 Noslip 求解器也是一个 PGS 求解器，因此只要启用了 Noslip，就会支付 PGS 的设置成本，即使主求解器是 CG 或牛顿算法。主 PGS 和 Noslip PGS 的设置操作是相同的，因此当两者都启用时，设置成本只支付一次。

执行器#

本节描述了在 MuJoCo 中使用执行器的各个方面。有关计算模型，请参阅驱动模型。

分组禁用#

actuatorgroupdisable 属性可以通过设置 mjOption.disableactuator 整数位字段在运行时更改，它允许用户根据执行器的组来禁用执行器集。当人们想为同一个运动学树使用多种类型的执行器时，此功能很方便。例如，考虑一个固件支持多种控制模式的机器人，例如力矩控制和位置控制。在这种情况下，可以在同一个 MJCF 模型中定义两种类型的执行器，将一种类型的执行器分配给组 0，另一种分配给组 1。

actuatorgroupdisable MJCF 属性选择默认禁用的组，并且可以在运行时设置 mjOption.disableactuator 来切换活动集。请注意，执行器的总数 mjModel.nu 保持不变，执行器索引也一样，因此用户需要知道被禁用的执行器的相应 mjData.ctrl 值将被忽略并且不产生力。这个示例模型有三个执行器组，可以在 simulate 交互式查看器中在运行时切换。请参阅右侧的示例模型和相关的屏幕截图。

快捷方式#

正如在“计算”章节的驱动模型部分所解释的，MuJoCo 提供了一个灵活的执行器模型，其传动、激活动力学和力生成组件可以独立指定。完整的功能可以通过 XML 元素 general 访问，它允许用户创建各种自定义执行器。此外，MJCF 提供了用于配置常见执行器的快捷方式。这是通过 XML 元素 motor、position、velocity、intvelocity、damper、cylinder、muscle 和 adhesion 完成的。这些不是独立的模型元素。在内部，MuJoCo 只支持一种执行器类型——这就是为什么当保存 MJCF 模型时，所有执行器都写为 general。快捷方式隐式地创建通用执行器，将其属性设置为合适的值，并以可能不同的名称公开其属性的子集。例如，position 创建一个位置伺服，其属性 kp 是伺服增益。然而，general 没有属性 kp。相反，解析器以协调的方式调整通用执行器的增益和偏置参数，以模仿位置伺服。通过直接使用 general 并将其属性设置为下面描述的某些值，可以实现相同的效果。

执行器快捷方式也与默认值交互。回想一下，默认设置机制涉及类，每个类都有一套完整的虚拟元素（每种元素类型一个），用于初始化实际模型元素的属性。特别是，每个默认类只有一个通用执行器元素。如果我们在同一个默认类中先指定 position 然后再指定 velocity 会发生什么？XML 元素按顺序处理，每次遇到与执行器相关的元素时，单个通用执行器的属性都会被设置。因此，velocity 具有优先权。但是，如果我们在默认类中指定 general，它将只设置明确给出的属性，并保持其余属性不变。在创建实际模型元素时也会出现类似的复杂情况。假设活动默认类指定了 position，现在我们使用 general 创建一个执行器并省略了它的一些属性。缺失的属性将被设置为用于模拟位置伺服的任何值，即使该执行器可能不打算作为位置伺服。

鉴于这些潜在的复杂性，我们推荐一种简单的方法：在默认类和创建实际模型元素时都使用相同的执行器快捷方式。如果给定模型需要不同的执行器，要么创建多个默认类，要么避免对执行器使用默认值，而是明确指定其所有属性。

力限制#

执行器的力通常被限制在下限和上限之间。这些限制可以通过三种方式强制执行

使用 ctrlrange 进行控制钳位

如果设置了此执行器属性，输入控制值将被钳位。对于简单的电机，钳位控制输入等同于钳位力输出。

使用 forcerange 在执行器输出端进行力钳位

如果设置了此执行器属性，执行器的输出力将被钳位。此属性对于例如位置执行器很有用，以将力保持在界限内。请注意，位置执行器通常还需要控制范围钳位以避免达到关节限制。

使用 joint/actuatorfrcrange 在关节输入端进行力钳位

此关节属性钳位来自所有作用于该关节的执行器的输入力，这些力在通过传动后。如果在执行器和关节之间存在一对一关系（即传动是平凡的），则在关节处钳位执行器力等同于在执行器处钳位它们。然而，在多个执行器作用于一个关节或一个执行器作用于多个关节的情况下——但实际的扭矩是由关节处的单个物理执行器施加的——最好在关节本身钳位力。以下是三个希望在关节而非执行器处钳位执行器力的例子

在这个示例模型中，两个执行器，一个电机和一个阻尼器，作用于单个关节。
在这个示例模型中（类似于“Dubin's Car”），两个执行器通过固定肌腱传动作用于两个车轮，以施加对称（前进/后退）和反对称（右转/左转）的扭矩。
在这个示例模型中，一个站点传动实现了一个手臂末端执行器的笛卡尔控制器。为了使计算出的扭矩能够由单个、扭矩受限的关节电机实现，它们需要在关节处被钳位。

请注意，在这种情况下，当力/扭矩由传动组合时，应使用 jointactuatorfrc 传感器来报告作用于关节的总执行器力。标准的 actuatorfrc 传感器将继续报告钳位前的执行器力。

使用 tendon/actuatorfrcrange 在肌腱输入端进行力钳位

此肌腱属性钳位所有作用于该肌腱的执行器的输入力。

上述钳位选项不是互斥的，可以根据需要组合使用。

长度范围#

字段 mjModel.actuator_lengthrange 包含可行的执行器长度范围（或者更准确地说，是执行器传动的长度）。这对于模拟肌肉执行器是必需的。在这里，我们关注 actuator_lengthrange 的含义以及如何设置它。

与 mjModel 中所有其他表示精确物理或几何量的字段不同，actuator_lengthrange 是一个近似值。直观上，它对应于执行器的传动在所有“可行”模型配置下可以达到的最小和最大长度。然而，MuJoCo 的约束是软的，所以原则上任何配置都是可行的。但我们仍然需要一个明确定义的范围来进行肌肉建模。有三种方法可以设置这个范围：(1) 使用所有执行器中新增的属性 lengthrange 显式提供它；(2) 从执行器所附着的关节或肌腱的限制中复制它；(3) 自动计算它，如本节其余部分所解释。这里有很多选项，由新的 XML 元素 lengthrange 控制。

执行器长度范围的自动计算在编译时完成，结果存储在编译后模型的 mjModel.actuator_lengthrange 中。如果模型随后被保存（无论是 XML 还是 MJB 格式），下次加载时就不需要重复计算。这很重要，因为对于大型肌肉骨骼模型，这个计算可能会减慢模型编译器的速度。事实上，我们已经将编译器设为多线程，就是为了加速这个操作（不同的执行器在不同的线程中并行处理）。

自动计算依赖于修改后的物理仿真。对于每个执行器，我们通过其传动施加力（计算最小值时为负，计算最大值时为正），在阻尼状态下推进仿真以避免不稳定性，给它足够的时间稳定下来并记录结果。这与带动量的梯度下降有关，实际上我们也尝试过基于显式梯度的优化，但问题在于不清楚我们应该优化什么目标（考虑到软约束的混合）。通过使用仿真，我们实际上是让物理告诉我们该优化什么。但请记住，这仍然是一个优化过程，因此它有需要调整的参数。我们提供了保守的默认值，应该适用于大多数模型，但如果它们不适用，请使用 lengthrange 的属性进行微调。

在使用此功能时，记住模型的几何形状很重要。这里的隐含假设是，可行的执行器长度确实是有限的。此外，我们不将接触视为限制因素（事实上，我们在此仿真中内部禁用了接触，以及被动力、重力、摩擦损失和执行器力）。这是因为带有接触的模型可能会缠结并产生许多局部最小值。因此，执行器应该受限于模型中定义的关节或肌腱限制（在此仿真期间启用）或由于几何形状。为了说明后者，考虑一个肌腱，一端连接到世界，另一端连接到一个围绕附着在世界上的铰链关节旋转的物体。在这种情况下，肌腱的最小和最大长度是明确定义的，并且取决于附着点在空间中描绘的圆的大小，即使关节和肌腱都没有用户定义的限制。但是如果执行器附着在关节上，或者附着在等于关节的固定肌腱上，那么它是无限的。在这种情况下，编译器会返回一个错误，但它无法判断错误是由于不收敛还是因为执行器长度无限。所有这些听起来过于复杂，从某种意义上说，我们正在考虑所有可能的极端情况。在实践中，长度范围几乎总是与附着在空间肌腱上的肌肉执行器一起使用，并且模型中会定义关节限制，从而有效地限制肌肉执行器的长度。如果你在这样的模型中遇到收敛错误，最可能的解释是你忘记了包含关节限制。

有状态的执行器#

如“计算”章节的驱动模型部分所述，MuJoCo 支持具有内部动力学的驱动器，其状态称为“激活”。

激活限制#

有状态驱动器的一个有用应用是“积分速度”驱动器，通过 intvelocity 快捷方式实现。与对传动目标速度进行直接反馈的纯速度驱动器不同，积分速度驱动器将一个积分器与一个位置反馈驱动器耦合。在这种情况下，激活状态的语义是“位置驱动器的设定点”，而控制信号的语义是“位置驱动器设定点的速度”。请注意，在真实的机器人系统中，这种积分速度驱动器是具有速度语义的驱动器最常见的实现方式，而不是对速度的纯反馈，因为后者通常非常不稳定（无论是在现实生活中还是在仿真中）。

在积分速度驱动器的情况下，通常需要钳制激活状态，否则位置目标会持续积分超出关节限制，导致可控性丧失。要查看激活钳制的效果，请加载下面的示例模型。

带激活限制的示例模型

<mujoco>
<default>
   <joint axis="0 0 1" limited="true" range="-90 90" damping="0.3"/>
   <geom size=".1 .1 .1" type="box"/>
</default>

<worldbody>
   <body>
      <joint name="joint1"/>
      <geom/>
   </body>
   <body pos=".3 0 0">
      <joint name="joint2"/>
      <geom/>
   </body>
</worldbody>

<actuator>
   <general name="unclamped" joint="joint1" gainprm="1" biastype="affine"
      biasprm="0 -1" dyntype="integrator"/>
   <intvelocity name="clamped" joint="joint2" actrange="-1.57 1.57"/>
</actuator>
</mujoco>

请注意，actrange 属性始终以原生单位（弧度）指定，即使关节范围可以是度（默认）或弧度，这取决于 compiler/angle 属性。

肌肉#

我们提供了一套用于模拟生物肌肉的工具。希望以最少努力添加肌肉的用户可以通过在驱动器部分添加一行 XML 来实现。

<actuator>
    <muscle name="mymuscle" tendon="mytendon">
</actuator>

生物肌肉彼此看起来非常不同，但在应用了某种缩放后，它们的行为却惊人地相似。我们的默认设置应用了这种缩放，这就是为什么可以在不调整任何参数的情况下获得合理的肌肉模型。当然，构建更详细的模型需要调整参数，本节将对此进行解释。

请记住，尽管肌肉模型相当复杂，但它仍然是 MuJoCo 驱动器的一种，并遵循与其他所有驱动器相同的约定。肌肉可以使用 general 来定义，但快捷方式 muscle 更方便。与所有其他驱动器一样，力的产生机制和传动装置是独立定义的。然而，肌肉只有附着在肌腱或关节传动上才具有（生物）物理意义。为具体起见，我们在此假设使用肌腱传动。

首先我们讨论长度和长度缩放。传动装置（即 MuJoCo 肌腱）的可行长度范围将发挥重要作用；请参阅上面的长度范围部分。在生物力学中，肌肉和肌腱串联在一起，形成一个肌肉-肌腱驱动器。我们的约定略有不同：在 MuJoCo 中，具有空间属性（特别是长度和速度）的实体是肌腱，而肌肉是拉动肌腱的抽象力生成机制。因此，MuJoCo 中的肌腱长度对应于生物力学中的肌肉+肌腱长度。我们假设生物肌腱是无弹性的，具有恒定长度 \(L_T\)，而生物肌肉长度 \(L_M\) 随时间变化。MuJoCo 肌腱长度是生物肌肉和肌腱长度之和。

\[\texttt{actuator\_length} = L_T + L_M \]

另一个重要的常数是肌肉的最佳静息长度，表示为 \(L_0\)。它等于肌肉在零速度下产生最大主动力时的长度 \(L_M\)。我们不要求用户直接指定 \(L_0\) 和 \(L_T\)，因为考虑到肌腱布线和缠绕的空间复杂性，很难知道它们的数值。相反，我们自动计算 \(L_0\) 和 \(L_T\)，如下所示。上面描述的长度范围计算已经提供了 \(L_T+L_M\) 的操作范围。此外，我们要求用户指定肌肉长度 \(L_M\) 的操作范围，该范围由（仍然未知的）常数 \(L_0\) 缩放。这是通过属性 range 完成的；默认的缩放范围是 \((0.75, 1.05)\)。现在我们可以计算这两个常数，利用实际范围和缩放范围必须相互映射的事实：

\[\begin{aligned} (\texttt{actuator\_lengthrange[0]} - L_T) / L_0 &= \texttt{range[0]} \\ (\texttt{actuator\_lengthrange[1]} - L_T) / L_0 &= \texttt{range[1]} \\ \end{aligned} \]

在运行时，我们计算缩放后的肌肉长度和速度为：

\[\begin{aligned} L &= (\texttt{actuator\_length} - L_T) / L_0 \\ V &= \texttt{actuator\_velocity} / L_0 \\ \end{aligned} \]

缩放量的优点是所有肌肉在该表示中都表现相似。这种行为由许多实验论文中测量的力-长度-速度（\(\text{\small FLV}\)）函数捕获。我们如下近似该函数：

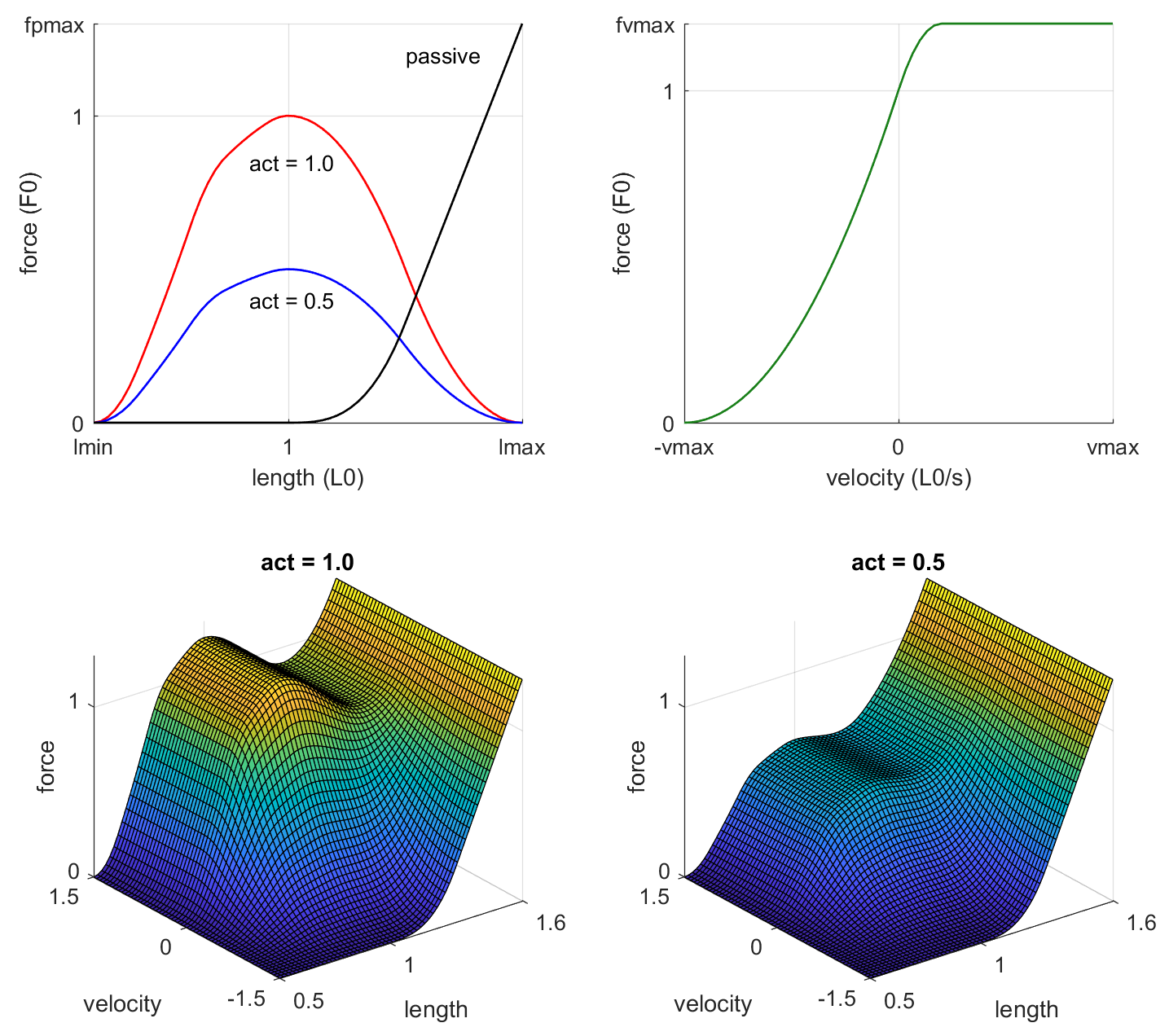
该函数的形式为：

\[\text{\small FLV}(L, V, \texttt{act}) = F_L(L)\cdot F_V(V)\cdot \texttt{act} + F_P(L) \]

与 MuJoCo 驱动器的一般形式相比，我们看到 \(F_L\cdot F_V\) 是驱动器增益，\(F_P\) 是驱动器偏置。\(F_L\) 是作为长度函数的主动力，而 \(F_V\) 是作为速度函数的主动力。它们相乘以获得总的主动力（注意由 act 缩放，act 是驱动器激活）。\(F_P\) 是被动力，无论激活与否都始终存在。\(\text{\small FLV}\) 函数的输出是缩放后的肌肉力。我们将缩放后的力乘以肌肉特定的常数 \(F_0\) 以获得实际的力：

\[\texttt{actuator\_force} = -\text{\small FLV}(L, V, \texttt{act}) \cdot F_0 \]

负号是因为正的肌肉激活会产生拉力。常数 \(F_0\) 是零速度下的峰值主动力。它与肌肉的厚度（即生理横截面积或 PCSA）有关。如果已知，可以使用 muscle 元素的 force 属性进行设置。如果未知，我们将其设置为 \(-1\)，这是默认值。在这种情况下，我们依赖于这样一个事实：较大的肌肉倾向于作用于移动更大重量的关节。scale 属性定义了这种关系：

\[F_0 = \text{scale} / \texttt{actuator\_acc0} \]

量 \(\texttt{actuator\_acc0}\) 由模型编译器预先计算。它是由作用在驱动器传动上的单位力引起的关节加速度的范数。直观地说，\(\text{scale}\) 决定了肌肉“平均”有多强，而其实际强度取决于整个模型的几何和惯性特性。

到目前为止，我们遇到了三个定义单个肌肉属性的常数：\(L_T, L_0, F_0\)。此外，函数 \(\text{\small FLV}\) 本身有几个参数，如上图所示：\(l_\text{min}, l_\text{max}, v_\text{max}, f_\text{pmax}, f_\text{vmax}\)。这些参数应该对所有肌肉都相同，但是不同的实验论文提出了不同形状的 FLV 函数，因此熟悉该文献的用户可能希望调整它们。我们提供了 MATLAB 函数 FLV.m，该函数用于生成上图，并展示了我们如何计算 \(\text{\small FLV}\) 函数。

在着手设计更精确的 \(\text{\small FLV}\) 函数之前，请考虑这样一个事实：肌肉的操作范围比 \(\text{\small FLV}\) 函数的形状影响更大，而且在许多情况下，这个参数是未知的。下面是一个图形说明：

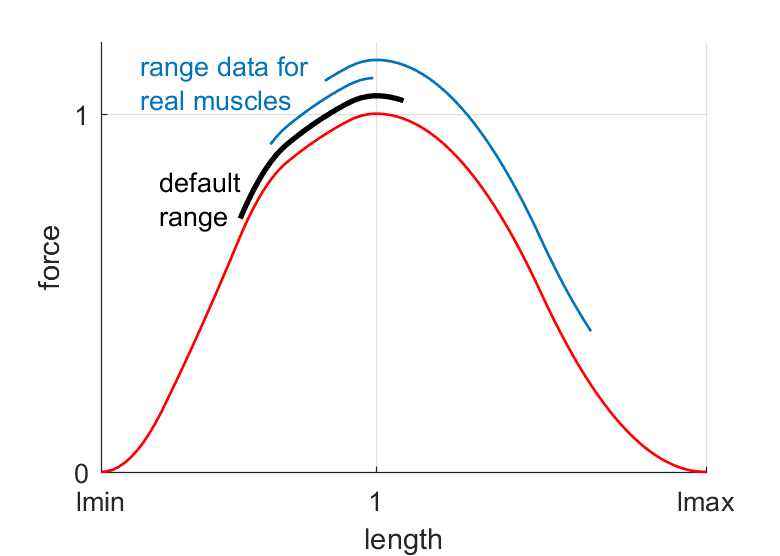
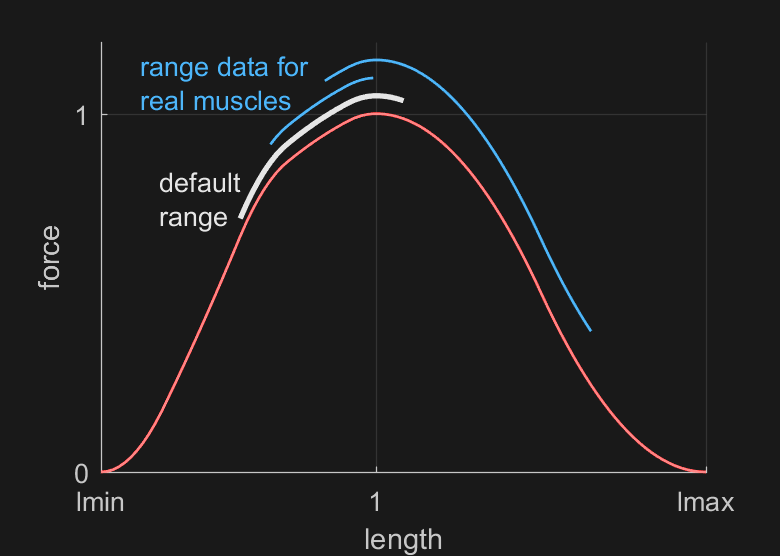
这种图表格式在生物力学文献中很常见，显示了每个肌肉的操作范围叠加在归一化的 \(\text{FL}\) 曲线上（忽略垂直位移）。我们的默认范围以黑色显示。蓝色曲线是两个臂部肌肉的实验数据。可以发现肌肉有小范围、大范围、跨越 \(\text{FL}\) 曲线的上升部分或下降部分，或两者兼有。现在假设你有一个包含 50 块肌肉的模型。你相信有人做了仔细的实验并测量了你模型中每块肌肉的操作范围，并考虑了肌肉跨越的所有关节吗？如果不是，那么最好将肌肉骨骼模型视为与生物系统具有相同的一般行为，但在各种细节上有所不同——包括某些研究社区非常感兴趣的细节。对于建模者认为恒定和已知的多数肌肉属性，都有实验论文表明它们在某些条件下会变化。这并不是要阻止人们建立精确的模型，而是要阻止人们过分相信自己的模型。

回到我们的肌肉模型，还有肌肉激活 act。这是一个一阶非线性滤波器的状态，其输入是控制信号。滤波器动力学为：

\[\frac{\partial}{\partial t}\texttt{act} = \frac{\texttt{ctrl} - \texttt{act}}{\tau(\texttt{ctrl}, \texttt{act})} \]

在内部，即使驱动器没有指定控制范围，控制信号也会被钳制在 [0, 1] 之间。有两个时间常数通过 timeconst 属性指定，即 \(\text{timeconst} = (\tau_\text{act}, \tau_\text{deact})\)，默认值为 \((0.01, 0.04)\)。遵循 Millard et al. (2013)，有效时间常数 \(\tau\) 在运行时计算如下：

\[\tau(\texttt{ctrl}, \texttt{act}) = \begin{cases} \tau_\text{act} \cdot (0.5 + 1.5\cdot\texttt{act}) & \texttt{ctrl}-\texttt{act} \gt 0 \\ \tau_\text{deact} / (0.5 + 1.5\cdot\texttt{act}) & \texttt{ctrl} - \texttt{act} \leq 0 \end{cases} \]

由于上述方程描述了不连续的切换，这在使用基于导数的优化时可能不理想，因此我们引入了可选的平滑参数 tausmooth。当大于 0 时，切换将由 mju_sigmoid 替换，它将在 \((\texttt{ctrl}-\texttt{act}) \pm \text{tausmooth}/2\) 范围内平滑地插值两个值。

现在我们总结一下用户可能想要调整的 muscle 元素的属性，这取决于他们对生物力学文献的熟悉程度以及关于特定模型的详细测量数据的可用性：

默认值: 在所有地方都使用内置的默认值。您所要做的就是将肌肉连接到肌腱上，如本节开头所示。这样可以得到一个通用但合理的模型。
scale: 如果您不知道单个肌肉的力量，但希望使所有肌肉更强或更弱，请调整 scale。这可以为每个肌肉单独调整，但在 default 元素中设置一次更有意义。
force: 如果您知道单个肌肉的峰值主动力 \(F_0\)，请在此处输入。许多实验论文都包含这些数据。
range: 肌肉在缩放长度下的操作范围也可以在一些论文中找到。尚不清楚这些测量的可靠性如何（考虑到肌肉作用于许多关节），但它们确实存在。请注意，不同肌肉的范围差异很大。
timeconst: 肌肉由慢缩肌纤维和快缩肌纤维组成。典型的肌肉是混合型的，但一些肌肉具有更高比例的某种纤维类型，使其更快或更慢。这可以通过调整时间常数来建模。\(\text{\small FLV}\) 函数的 vmax 参数也应相应调整。
tausmooth: 当为正值时，平滑激活和失活时间常数之间的过渡。虽然单个运动单元要么是激活状态，要么是失活状态，但整个肌肉将包含许多单元的混合，从而导致相应的时间尺度混合。
lmin、lmax、vmax、fpmax、fvmax: 这些是控制 \(\text{\small FLV}\) 函数形状的参数。高级用户可以尝试使用它们；请参阅 MATLAB 函数 FLV.m。与 scale 设置类似，如果您想更改所有肌肉的 \(\text{\small FLV}\) 参数，请在 default 元素中进行。
自定义模型: 用户可以实现一个不同的模型，而不是调整我们肌肉模型的参数，方法是将 general 驱动器的 gaintype、biastype 和 dyntype 设置为“user”，并在运行时提供回调。或者，将其中一些类型保留为“muscle”并使用我们的模型，同时替换其他组件。请注意，肌腱几何计算仍由标准 MuJoCo 管道处理，提供 actuator_length、actuator_velocity 和 actuator_lengthrange 作为用户肌肉模型的输入。然后，自定义回调可以模拟弹性肌腱或我们选择省略的任何其他细节。

与 OpenSim 的关系

生物力学研究人员使用的标准软件是 OpenSim。我们设计了我们的肌肉模型，使其在可能的情况下与 OpenSim 模型相似，同时进行了简化，从而实现了显著更快的速度和更稳定的模拟。为了帮助 MuJoCo 用户转换 OpenSim 模型，我们在此总结了相似之处和不同之处。

激活动力学模型与 OpenSim 相同，包括默认的时间常数。

FLV 函数不完全相同，但 MuJoCo 和 OpenSim 都近似于相同的实验数据，所以它们非常接近。有关 OpenSim 模型的描述和相关实验数据的摘要，请参见 Millard et al. (2013)。

我们假设肌腱是无弹性的，而 OpenSim 可以模拟肌腱弹性。我们决定不在这里这样做，因为肌腱弹性需要快速平衡假设，而这反过来又需要各种调整，并且容易导致模拟不稳定。实际上，肌腱非常坚硬，它们的影响可以通过拉伸对应于无弹性情况的 FL 曲线来近似捕获（Zajac (1989)）。这可以在 MuJoCo 中通过缩短肌肉操作范围来实现。

MuJoCo 中没有对羽状角（即肌肉与力线之间的角度）进行建模，并假设其为 0。这种效应可以通过缩小肌肉力并调整操作范围来近似。

肌腱包裹在 MuJoCo 中也更有限。我们允许球体和无限圆柱体作为包裹对象，并要求两个包裹对象之间由肌腱路径中的一个固定位点分隔。这是为了避免需要对肌腱路径进行迭代计算。我们还允许将“侧位点”放置在球体或圆柱体内，这会导致反向包裹：肌腱路径被约束为穿过对象而不是绕过它。这可以替代 OpenSim 中用于将肌腱路径保持在给定区域内的环形包裹对象。总的来说，肌腱包裹是将 OpenSim 模型转换为 MuJoCo 模型中最具挑战性的部分，需要一些手动工作。好的一面是，正在使用的高质量 OpenSim 模型数量很少，所以一旦它们被转换，我们就完成了。

下面我们说明了可用的四种肌腱包裹类型。请注意，包裹肌腱的弯曲部分被渲染为直线，但几何管道使用实际曲线工作，并解析地计算它们的长度和力矩。

传感器#

如以下 sensor 元素中所述，MuJoCo 可以模拟各种各样的传感器。也可以定义用户传感器类型，并通过回调 mjcb_sensor 进行评估。传感器不影响模拟。相反，它们的输出被复制到数组 mjData.sensordata 中，并可供用户处理。

在这里，我们描述了所有传感器类型共有的 XML 属性，以避免稍后重复。

name: string, optional: 传感器名称。
noise: real, “0”: 此传感器噪声模型的标准差。在 3.1.4 之前的版本中，这会导致噪声被添加到传感器中。在 3.1.4 版本中，此功能被移除，详细理由请参阅 3.1.4 更新日志。从后续版本开始，该属性可作为保存标准差信息以备后用的便捷位置。
cutoff: real, “0”: 当此值为正时，它会限制传感器输出的绝对值。它也用于在 simulate.cc 的传感器数据图中归一化传感器输出。
user: real(nuser_sensor), “0 0 …”: 请参阅用户参数。

相机#

除了默认的用户可控自由相机外，“固定”相机可以附加到运动学树上。

外参

默认情况下，相机坐标系附加到其所在的物体上。可选的 mode 和 target 属性可用于指定跟踪（随之移动）或瞄准（看向）某个物体或子树的相机。相机朝向相机坐标系的负 Z 轴，而正 X 和 Y 分别对应于图像平面中的*右*和*上*。

内参

相机内参使用 ipd（瞳孔间距，立体渲染和 VR 所需）和 fovy（垂直视场，以度为单位）指定。

上述规范意味着一个没有像差的完美针孔相机。然而，在校准真实相机时，两种类型的线性像差可以使用标准渲染管线来表示。第一种是垂直和水平方向上不同的焦距（轴对齐像散）。第二种是主点不居中。这些可以使用 focal 和 principal 属性来指定。当使用这些与校准相关的属性时，还必须指定物理传感器尺寸和相机分辨率。在这种情况下，可以可视化渲染视锥体。

复合对象#

复合对象不是新的模型元素。相反，它们是现有元素的集合，最初设计用于模拟粒子系统、绳索、布料和软体。随着时间的推移，这些类型中的大多数已被 replicate（用于重复对象）和 flexcomp（用于软对象）所取代。因此，现在唯一支持的复合类型是 cable，它产生一个由球形关节连接的不可伸展的物体链。

复合对象由常规的 MuJoCo 物体组成，在此上下文中我们称之为“元素物体”。元素物体的集合由模型编译器自动生成。用户使用新的 XML 元素 composite 及其属性和子元素，在较高层次上配置自动生成器，如 XML 参考章节所述。如果编译后的模型被保存，composite 将不再存在，而是被自动生成的常规模型元素集合所取代。因此，可以将其视为一个由模型编译器展开的宏。元素物体作为 composite 所在的物体的子物体被创建；因此，复合对象出现在 XML 中可能定义常规子物体的位置。每个自动生成的元素物体都附加了一个几何体。我们设计了复合对象生成器，使其具有尽可能直观的高级控制，但同时它也暴露了大量相互作用的选项，这些选项可以深刻影响最终的物理效果。因此，在某个时候，用户应该仔细阅读参考文档。

除了设置物理特性外，复合对象生成器还创建合适的渲染效果。对象可以渲染为皮肤。皮肤是自动生成的，可以进行纹理贴图以及使用双三次插值进行细分。实际的物理特性，特别是碰撞检测，是基于元素物体及其几何体的，而皮肤纯粹是一个可视化对象。然而，在某些情况下，我们更喜欢看皮肤表示，如在这个模型中，其皮肤是一个连续的柔性表面，而不是一堆不连续的薄盒子。然而，在微调模型并试图理解其背后的物理原理时，能够渲染几何体是很有用的。要切换渲染风格，请禁用皮肤的渲染，并为几何体和肌腱启用组 3。

缆绳.

作为快速入门，MuJoCo 提供了一个复合缆绳的示例。在所有示例中，我们都有一个包含在模型中的静态场景，后面跟着一个单一的复合对象。下面的 XML 片段只是复合对象的定义；请参阅发行版中的 XML 模型文件以获取完整示例。

<extension>
   <plugin plugin="mujoco.elasticity.cable"/>
</extension>

<worldbody>
   <composite prefix="actuated" type="cable" curve="cos(s) sin(s) s" count="41 1 1"
              size="0.25 .1 4" offset="0.25 0 .05" initial="none">
      <plugin plugin="mujoco.elasticity.cable">
         <!--Units are in Pa (SI)-->
         <config key="twist" value="5e8"/>
         <config key="bend" value="15e8"/>
         <config key="vmax" value="0"/>
      </plugin>
      <joint kind="main" damping="0.15" armature="0.01"/>
      <geom type="capsule" size=".005" rgba=".8 .2 .1 1"/>
   </composite>
</worldbody>

缆绳模拟了一个具有扭转和弯曲刚度的不可伸展的弹性一维物体。它使用一系列胶囊体或盒子进行离散化。其刚度和惯性特性直接根据给定的参数和横截面的形状计算，从而允许各向异性行为，例如在皮带或计算机电缆中可以找到。它是一个单一的运动学树，因此在不使用额外约束的情况下是完全不可伸展的，从而可以使用大的时间步长。弹性模型是几何精确的，基于计算中心线的主教标架或无扭转标架，即穿过横截面中心的线。几何体的方向是相对于该标架表示的，然后分解为扭转和弯曲分量，因此可以独立设置不同的刚度。此外，可以指定无应力配置是平坦的还是弯曲的，例如在螺旋弹簧的情况下。缆绳需要使用第一方引擎插件，该插件将来可能会直接集成到引擎中。

粒子.

粒子类型已弃用。建议使用更通用的 replicate 代替，例如此模型。

网格.

网格复合类型已被移除。建议使用二维柔性可变形对象来模拟薄弹性结构。

绳索和环.

绳索和环已弃用。建议使用缆绳模拟弯曲和扭曲的不可伸展弹性杆，以及在拉伸加载场景中使用一维柔性可变形对象来模拟可伸展的弦（例如拉伸的橡皮筋）。

布料.

布料已弃用。建议使用二维柔性可变形对象来模拟薄弹性结构。

盒子、圆柱体和椭球体.

盒子类型以及圆柱体和椭球体类型现已弃用，推荐使用三维柔性可变形对象。

可变形对象#

前面描述的复合对象旨在在一个实际上是刚体模拟器中模拟软体。这是可能的，因为 MuJoCo 的约束是软的，但它在功能和建模能力上仍然受到限制。在 MuJoCo 3.0 中，我们引入了涉及新模型元素的真正可变形对象。前面描述的皮肤实际上就是这样一个元素，但它仅用于可视化。我们现在有一个相关的元素 flex，它可以根据需要生成接触力、约束力和被动力，以模拟各种可变形实体。皮肤和柔性体现在都在 XML 中一个新的分组元素 deformable 中定义。柔性体是一个低级元素，它指定了运行时所需的一切，但在建模时很难设计。为了帮助建模，我们进一步引入了元素 flexcomp，它自动化了低级柔性体的创建，类似于 composite 自动化创建模拟软体所需的 MuJoCo 对象（集合）的方式。柔性体最终可能会取代复合体，但目前两者在某种程度上用于不同的目的。

柔性体是 MuJoCo 物体的集合，这些物体通过无质量的可伸展元素连接。这些元素可以是胶囊（一维柔性体）、三角形（二维柔性体）或四面体（三维柔性体）。在所有情况下，我们都允许一个半径，这使得元素变得平滑，并且在一维和二维中也具有体积。原始元素如下图所示。

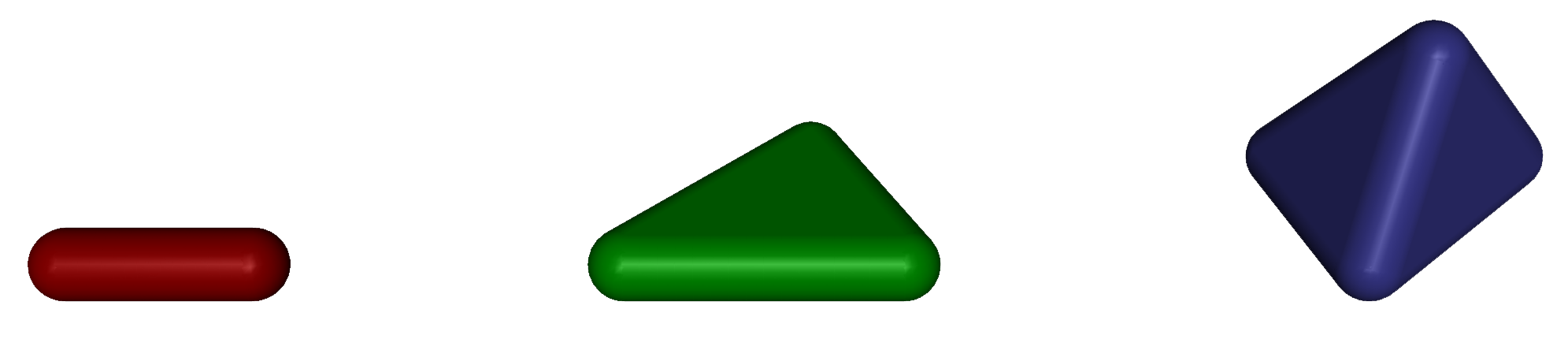
到目前为止，这些看起来像几何体。但关键的区别在于它们会变形：当物体（顶点）相互独立移动时，元素的形状会实时改变。碰撞和接触力现在被推广以处理这些可变形的几何元素。请注意，当两个这样的元素碰撞时，接触不再只涉及两个物体，而是可能涉及多达 8 个物体（如果两个元素都是四面体）。接触力的计算方式与以前一样，给定接触框架和在该框架中表示的相关量。但随后接触力会分布到所有相互作用的物体上。接触雅可比的概念变得复杂，因为接触点不能被认为是固定在任何物体框架中的。相反，我们使用一种加权方案来将每个接触点“分配”给多个物体。也可以通过将所有顶点分配给同一个物体来创建一个刚性柔性体。这是重新利用新的柔性碰撞机制来实现刚性非凸网格碰撞的一种方式（与为碰撞目的而凸化的网格几何体不同）。

变形模型.

为了（以软约束的方式）保持柔性体的形状，我们需要生成被动力或约束力。在 MuJoCo 3.0 之前，这会涉及到大量的肌腱以及对肌腱和关节的约束。在这里这仍然是可能的，但是当柔性体很大时，在建模和模拟方面效率都很低。相反，设计理念是使用一组参数并提供两种建模选择：一种新的（软）等式约束类型，适用于给定柔性体的所有边，允许大的时间步长；或者一种离散化的连续介质表示，其中每个元素都处于恒定应力状态，这等效于分段线性有限元，并实现了更高的真实性和准确性。基于边的模型可以看作是一个“集总”刚度模型，其中变形模式（例如剪切和体积）的正确耦合被平均为一个单一的量。而连续介质模型则允许使用材料的泊松比分别指定剪切和体积刚度。更多细节，请参阅圣维南-基尔霍夫超弹性模型。

创建和可视化.

<option timestep=".001"/>

<worldbody>
   <flexcomp type="grid" count="24 4 4" spacing=".1 .1 .1" pos=".1 0 1.5"
             radius=".0" rgba="0 .7 .7 1" name="softbody" dim="3" mass="7">
      <contact condim="3" solref="0.01 1" solimp=".95 .99 .0001" selfcollide="none"/>
      <edge damping="1"/>
      <elasticity poisson="0.2" young="5e4">
   </flexcomp>
</worldbody>

使用 flexcomp 元素，我们可以从网格（包括四面体网格）创建柔性体，并自动生成所有物体/顶点，并用合适的元素连接它们。我们还可以自动创建网格和其他拓扑结构。这种机制使得创建非常大的柔性体变得容易，涉及数千甚至数万个物体、元素和边。显然，这样的模拟不会很快。即使对于中等大小的柔性体，修剪碰撞对也是至关重要的。这就是为什么我们开发了复杂的自碰撞修剪方法；请参阅 XML 参考。

在由四面体构成的三维柔性体的情况下，检查柔性体内部是如何“三角化”的可能会很有用。我们有一个特殊的可视化模式，可以剥离外层。下面是斯坦福兔子的一个例子。请注意它外部有较小的四面体，内部有较大的四面体。这种网格设计是合理的，因为我们希望碰撞表面是准确的，但在内部我们只需要软材料属性——这需要较低的空间分辨率。为了将表面网格转换为四面体网格，我们推荐使用像 fTetWild 库这样的开源工具。

包含文件#

MJCF 文件可以使用 include 元素包含其他 XML 文件。从机制上讲，解析器会将主文件中对应于 include 元素的 DOM 节点替换为被包含文件中顶层元素子元素的 XML 元素列表。顶层元素本身会被丢弃，因为它在 XML 中是一个分组元素，如果被包含，将违反 MJCF 格式。

此功能支持模块化的 MJCF 模型；请参阅模型库中的 MPL 系列模型。模块化的一个例子是构建一个机器人模型（这往往很复杂），然后将其包含在多个“场景”中，即定义机器人环境中物体的 MJCF 模型。另一个例子是创建一个包含常用资源（例如具有精心调整的 rgba 值的材料）的文件，并将其包含在多个引用这些资源的模型中。

被包含的文件不要求本身是有效的 MJCF 文件，但它们通常是。实际上，我们设计这个机制是为了允许 MJCF 模型被包含在其他 MJCF 模型中。为了实现这一点，即使在单个模型的上下文中语义上没有意义，也允许重复的 MJCF 部分。例如，我们允许运动学树有多个根（即多个 worldbody 元素），解析器会自动合并它们。否则将机器人包含到场景中是不可能的。

重复 MCJF 部分的灵活性是有代价的：应用于整个模型的全局设置，例如 compiler 的 angle 属性，可以被多次定义。MuJoCo 允许这样做，并使用在处理完所有 include 元素后，在复合模型中遇到的最后一个定义。因此，如果模型 A 以度为单位定义，模型 B 以弧度为单位定义，并且 A 在 B 的 compiler 元素之后被包含在 B 中，那么整个复合模型将被视为以度为单位定义——在这种情况下会导致不希望的后果。用户必须确保相互包含的模型在这方面是兼容的；局部坐标与全局坐标是另一个兼容性要求。

最后，如下文所述，元素名称在同类型的所有元素中必须是唯一的。因此，例如，如果在两个模型中使用了相同的几何体名称，并且一个模型被包含在另一个模型中，这将导致编译错误。多次包含同一个 XML 文件是一个解析错误。此限制的原因是我们希望避免重复的元素名称以及由包含引起的无限递归。

命名元素#

MJCF 中的大多数模型元素都可以有名称。它们是通过相应 XML 元素的 name 属性定义的。当给定的模型元素被命名时，其名称在同类型的所有元素中必须是唯一的。名称区分大小写。它们在编译时用于引用相应的元素，并且也保存在 mjModel 中，以便在运行时方便用户使用。

名称通常是一个可选属性。我们建议除非有特定原因，否则不要定义它（以保持模型文件更短）。可能有以下几个原因：

一些模型元素在创建时需要引用其他元素。例如，空间肌腱需要引用位点以指定其经过的路径点。引用只能通过名称进行。请注意，资源的存在就是为了被引用，因此它们必须有名称，但是可以省略它，并从相应的文件名中隐式设置。
可视化工具提供了标记给定类型的所有模型元素的选项。当名称可用时，它会打印在 3D 视图中的对象旁边；否则会打印一个通用标签，格式为“body 7”。
函数 mj_name2id 返回具有给定类型和名称的模型元素的索引。相反，函数 mj_id2name 根据索引返回名称。这对于涉及通过其 XML 中的名称识别的模型元素的自定义计算非常有用（而不是依赖于在模型编辑时可能会改变的固定索引）。
通过命名某些元素，模型文件原则上可以变得更具可读性。但是请记住，XML 本身有注释机制，该机制更适合实现可读性——特别是因为大多数文本编辑器提供语法高亮，可以检测 XML 注释。

URDF 扩展#

统一机器人描述格式（URDF）是一种流行的 XML 文件格式，许多现有机器人都已用其建模。这就是为什么我们实现了对 URDF 的支持，尽管它只能表示 MuJoCo 中可用模型元素的一个子集。除了标准的 URDF 文件外，MuJoCo 还可以加载具有自定义（从 URDF 的角度看）mujoco 元素作为顶层元素 robot 的子元素的文件。这个自定义元素可以有子元素 compiler、option、size，其功能与 MJCF 中相同，只是默认的编译器设置被修改以适应 URDF 的建模约定。特别是 compiler 扩展已证明非常有用，事实上，它的几个属性的引入是因为一些现有的 URDF 模型具有非物理的动力学参数，如果未经修改，MuJoCo 的内置编译器会拒绝这些参数。这个扩展也需要用来指定网格目录。另请注意，编译器属性 strippath、angle、fusestatic 和 discardvisual 对于 URDF 和 MJCF 有不同的默认值。

请注意，虽然 MJCF 模型由解析器根据自定义 XML 模式进行检查，但 URDF 模型则不然。即使是嵌入在 URDF 文件中的 MuJoCo 特定元素也不会被检查。因此，拼写错误的属性名会被静默忽略，如果拼写错误没有被注意到，可能会导致重大混乱。

以下是 URDF 模型扩展部分的一个示例：

<robot name="darwin">
  <mujoco>
    <compiler meshdir="../mesh/darwin/" balanceinertia="true" discardvisual="false"/>
  </mujoco>
  <link name="MP_BODY">
    ...
</robot>

上述扩展使 URDF 更加可用，但仍然有限。如果用户希望构建充分利用 MuJoCo 的模型，同时保持 URDF 兼容性，我们建议采用以下步骤。根据需要在 URDF 中引入扩展，加载它并将其保存为 MJCF。然后尽可能使用 include 元素向 MJCF 添加信息。这样，如果 URDF 被修改，相应的 MJCF 可以很容易地重新创建。然而，根据我们的经验，URDF 文件往往是静态的，而 MJCF 文件则经常被编辑。因此，在实践中，通常将 URDF 转换为 MJCF 一次就足够了，之后只使用 MJCF。

MoCap 物体#

mocap 物体是世界的静态子物体（即没有关节），并且其 mocap 属性设置为“true”。它们可用于将来自运动捕捉设备的数据流输入到 MuJoCo 仿真中。假设您正拿着一个 VR 控制器，或一个装有运动捕捉标记（例如 Vicon）的物体，并希望有一个以相同方式移动但也能与其他模拟物体交互的模拟物体。这里有一个两难的境地：虚拟物体不能推你的物理手，所以你的手（以及你控制的物体）可能会违反模拟的物理定律。但同时我们希望最终的模拟是合理的。我们该怎么做呢？

第一步是在 MJCF 模型中定义一个 mocap 物体，并实现代码，在运行时读取数据流，并将 mjModel.mocap_pos 和 mjModel.mocap_quat 设置为从运动捕捉系统接收到的位置和方向。simulate.cc 代码示例使用鼠标作为运动捕捉设备，允许用户移动 mocap 物体。

关于 mocap 物体需要理解的关键是，模拟器将它们视为固定的。我们通过直接更新它们的位置和方向，使它们在一个模拟时间步到下一个时间步之间移动，但就物理模型而言，它们的位置和方向是恒定的。那么，如果我们与一个常规的动态物体接触会发生什么，就像 MuJoCo 发行版提供的粒子示例中那样（回想一下，在这些示例中，我们有一个胶囊探针，它是一个 mocap 物体，我们用鼠标移动它）。两个常规物体之间的接触会经历穿透和相对速度，而与 mocap 物体的接触则缺少相对速度分量，因为模拟器不知道 mocap 物体本身在移动。因此，产生的接触力较小，需要更长的时间才能将动态物体推开。此外，在更复杂的模拟中，我们做的与物理不一致的事情可能会导致不稳定。

然而，有一种行为更好的替代方案。除了 mocap 物体外，我们还包括第二个常规物体，并用焊接等式约束将其连接到 mocap 物体。在下图中，粉色盒子是 mocap 物体，它连接到手的底部。在没有其他约束的情况下，手几乎完美地跟踪 mocap 物体（并且比弹簧-阻尼器好得多），因为约束是隐式处理的，可以产生大的力而不会使模拟不稳定。但是，如果手被迫与桌子接触（右图），它就不能同时遵守接触约束和跟踪 mocap 物体。这是因为 mocap 物体可以自由地穿过桌子。那么哪个约束会胜出呢？这取决于焊接约束相对于接触约束的柔度。需要调整相应的 solref 和 solimp 参数以实现期望的权衡。有关示例，请参阅 MuJoCo 论坛上提供的模块化假肢（MPL）手部模型；下图是使用该模型生成的。

内存分配#

MuJoCo 在 mjData 中预分配了运行时所需的所有内存，并且在模型创建后不再访问堆分配器。mjData 中的内存由 mj_makeData 在两个连续的块中分配：

mjData.buffer 包含固定大小的数组。
mjData.arena 包含动态大小的数组。

在 arena 内存空间中分配了两种类型的动态数组。

接触和与约束相关的数组从 arena 的开头开始布局。
堆栈数组从 arena 的末尾开始布局。

通过从 arena 空间的两端分配动态量，可变大小的内存分配由一个单一的数字控制：size MJCF 元素的 memory 属性。与 buffer 中的固定大小数组不同，arena 中的可变大小数组可以是 NULL，例如在调用 mj_resetData 之后。当 arena 内存耗尽时，会发生以下三种情况之一，具体取决于请求的内存类型：

如果在接触分配期间内存耗尽，将发出警告，并且后续接触将不会在此步骤中添加，但模拟将照常继续。
如果在与约束相关的分配期间内存耗尽，将发出警告，并且约束求解器将在此步骤中被禁用，但模拟将照常继续。请注意，没有约束求解器的物理通常会非常不同，但允许模拟继续仍然可能有用，例如在场景初始化期间，当许多物体暂时重叠时。
如果在堆栈数组分配期间内存耗尽，将发生硬错误。

与 buffer 的大小不同，arena 的大小无法预先计算，因为接触数量和堆栈使用情况事先未知。那么应该如何选择它呢？目前使用以下简单的启发式方法，尽管将来可能会改进：在最坏情况下，为 100 个接触和 500 个标量约束分配足够的内存。如果此启发式方法不足，我们建议采用以下步骤。使用 memory 属性显著增加 arena 内存，并检查运行时的实际内存使用情况。mjData.maxuse_arena 跟踪自上次重置以来的最大 arena 内存利用率。simulate 查看器将此数字显示为总 arena 空间的一部分（在左下角的信息窗口中）。因此，可以从一个大的数字开始，模拟一段时间，如果分数很小，则返回 XML 并减少分配大小。但请记住，内存利用率在模拟过程中可能会发生巨大变化，这取决于有多少约束处于活动状态以及使用哪个约束求解器。CG 求解器是内存效率最高的，其次是牛顿求解器，而 PGS 求解器是内存最密集的。当我们设计模型时，我们通常的目标是在探索模型时遇到的最坏情况下达到 50% 的利用率。如果您只打算使用 CG 求解器，则可以使用显著更小的 arena 分配。

注意

内存分配行为在 MuJoCo 2.3.0 中发生了变化。在此版本之前，size MJCF 元素的 njmax、nconmax 和 nstack 属性的语义分别是为接触、约束和堆栈分配的最大内存。如果您使用的是早期版本的 MuJoCo，请切换到早期的文档版本以了解以前的行为。

提示与技巧#

在这里，我们提供了关于如何完成一些常见建模任务的指导。这里没有新内容，因为本节中的所有内容都可以从文档的其余部分推断出来。然而，推断过程并不总是显而易见的，所以将其详细说明可能会有所帮助。

性能调优#

以下是为最大化模拟吞吐量可以采取的一系列步骤。所有建议都涉及参数调整。建议在查看 simulate 实用程序的内置分析器时以交互方式进行这些操作。testspeed 实用程序也报告了详细且有时更有用的分析。在开始下面更复杂的步骤时，请针对分析器报告的最昂贵的流水线组件。请注意，其中一些对于 MJX 略有不同，请参阅其中的专门章节。

时间步：尝试增加模拟时间步。如数值积分部分末尾所述，时间步是任何模型中最重要的单个参数。默认值是为稳定性而非效率而选择的，通常可以增加。在某个点上，进一步增加它会导致发散，因此最佳时间步是发散从不发生或非常罕见的最大时间步。实际值取决于模型。
积分器：根据数值积分部分末尾的建议选择您的积分器。默认推荐的选择是 implicitfast 积分器。
约束雅可比：尝试在“dense”和“sparse”之间切换雅可比设置。这两个选项使用不同的代码路径，分别使用密集或稀疏代数，但在计算上是相同的，因此总是首选较快的一个。默认的“auto”启发式并不总能做出正确的选择。
约束求解器： 如果分析器报告求解器花费了大量时间，请考虑以下几点：
- 求解器：默认的牛顿求解器通常是最快的，因为它需要最少的迭代次数来收敛。对于大型模型，CG 求解器可能更快；对于自由度多于约束的模型，PGS 求解器将是最快的，尽管这种情况不常见。
- 迭代次数和容差：尝试减少迭代次数，或者等效地，增加求解器的终止容差。特别是对于牛顿求解器，它通常在 2-3 次（昂贵的）迭代中达到数值收敛，最后一次迭代将精度提高到一个没有明显效果的水平，可以跳过。
碰撞： 如果分析器报告碰撞检测占用了大量的计算时间，请考虑以下步骤：
- 使用碰撞检测部分中描述的 contype / conaffinity 机制减少检查的碰撞数量。
- 修改碰撞几何体，用更便宜的基元-基元碰撞替换昂贵的碰撞测试（例如网格-网格）。根据经验，在 engine_collision_driver.c 顶部的碰撞表中有自定义配对函数的碰撞比使用通用凸-凸碰撞器 mjc_Convex 的碰撞要便宜得多。最昂贵的碰撞是涉及 SDF 几何体的碰撞。
- 如果用基元替换碰撞网格不可行，请尽可能地简化网格。像 trimesh、Blender、MeshLab 和 CoACD 这样的开源工具在这方面非常有用。
摩擦锥：椭圆锥更准确，并且在高 impratio 下能更好地防止滑动，但计算成本更高。如果精确的摩擦不重要，可以尝试切换到棱锥。
使用 32 位浮点精度（而不是默认的 64 位）编译 MuJoCo。对于在多线程模式下运行的大型模型，其中内存访问比计算更昂贵，这可以带来（高达）2 倍的性能提升。有关更多信息，请参阅 mjtNum。

防止滑动#

以下是诊断和解决接触滑移问题可以采取的一系列步骤，这在操纵任务中尤其成问题。为了诊断滑移，建议使用 simulate 实用程序的内置可视化选项来检查接触和接触力。调整接触和力的视觉大小（使用全局 meansize 或特定的 contactwidth、contactheight 和 forcewidth 属性）和力缩放属性通常很有帮助，以便更好地可视化和理解接触配置和产生的力。

防滑接触力在摩擦锥之外

这意味着即使在理论上，物理学也无法防止滑动。这种情况发生在：

法向力太小。 确保夹持器可以施加的最大力乘以滑动摩擦系数明显大于物体的重量。
滑动摩擦系数太低。 增加滑动摩擦系数。
扭转摩擦不足以施加所需的扭矩。 将 condim 增加到 4 或 6，并选择适当的摩擦系数。condim 4 启用扭转摩擦，防止围绕法线旋转。condim 6 还启用滚动摩擦，防止围绕切线方向旋转。有关详细信息和这些系数的具体语义，请参阅接触部分。

几何形状不支持所需的力或扭矩

这是一个常见的现实世界问题，通过改进夹持器和手柄的设计来解决。

改进接触几何体的几何形状以增加更多接触点，可能使用非平面几何（例如，凸起），以便滑动由法向力而不仅仅是摩擦分量来防止。
如果接触是在平面之间，请尝试启用 multiccd 标志，它允许检测器找到比凸-凸碰撞器返回的单个接触更多的接触。
尝试通过设置 nativeccd 标志来启用原生碰撞检测管道，它使用更准确、更高效的凸碰撞检测算法。

高频振动

高频、低幅度的振动在许多工业环境中也是一个现实世界的问题，但与模拟不同，在现实世界中它们是可听见的。这种振动通常是由增益非常高的控制器引起的，有时也由接触或关节的粘滑反馈引起，与机构的本征模共振。诊断这种振动的最简单方法是在 simulate 中可视化接触力。解决方案通常是减小时间步和/或为相关关节添加一些电枢。振动的另一个原因是来自显式阻尼的反馈。使用隐式或 implicitfast 积分器，如数值积分部分所述。

缓慢滑动

与上述导致快速滑动的问题不同，缓慢、渐进的滑动是 MuJoCo 接触模型设计上的一个特性，因为没有它，逆动力学就无法定义。这在柔度和滑动澄清中有详细讨论。这种类型的滑动可以通过两种方式解决。

增加 impratio 参数。这将减少（但不能完全防止）缓慢滑动。请注意，高的 impratio 值仅与椭圆锥配合良好。
通过将 noslip_iterations 增加到正整数来启用 noslip 求解器。一个小的数字（1、2 或 3）通常就足够了。noslip 后处理求解器将完全防止滑动，但代价是使逆动力学变得不适定并增加额外的计算成本。

齿隙#

许多机器人关节都存在齿隙。它通常是由齿轮箱中齿轮之间的微小间隙引起的，但也可能是由关节机构中的某些松动引起的。其效果是，电机可以在关节转动之前转动一个小角度，或者反之亦然（当外力施加在关节上时）。齿隙可以在 MuJoCo 中建模如下。不是在物体内部只有一个铰链关节，而是定义两个具有相同位置和方向的铰链关节：

<body>
  <joint name="J1" type="hinge" pos="0 0 0" axis="0 0 1" armature="0.01"/>
  <joint name="J2" type="hinge" pos="0 0 0" axis="0 0 1" limited="true" range="-1 1"/>
</body>

因此，物体相对于其父物体的总旋转是 J1+J2。现在定义一个仅作用于 J1 的驱动器。J2 上的小关节范围使其保持在 0 附近，但允许它在作用于其上的力的方向上移动一点，从而产生齿隙效应。注意 J1 中的 armature 属性。没有它，关节空间惯性矩阵将是奇异的，因为两个关节可以向相反方向加速而不会遇到任何惯性。负责齿隙的物理齿轮实际上具有旋转惯量（我们称之为电枢），所以这是一种现实的建模方法。此示例中的数字应进行调整以获得期望的行为。关节限制约束的 solref 和 solimp 参数也可以调整，以使齿隙旋转在更软或更硬的限制处结束。

除了在 J2 中指定关节限制外，还可以指定一个软等式约束来保持 J2=0。然后应调整约束阻抗函数，使约束在 J2=0 附近较弱，而在远离 0 时变强。在求解器参数中展示的阻抗函数新参数化可以实现这一点。与关节限制相比，等式约束方法将在齿隙状态和限制状态之间产生更平滑的过渡。它也将一直处于活动状态，这对于需要约束违反或约束力作为输入的自定义代码来说很方便。

恢复#

存在另一种指定 solref 的机制，详见求解器参数。当两个数字都为非正数时，它们被解释为（-刚度，-阻尼）并按约束阻抗进行缩放。为了实现接触和其他约束的完美恢复，请将刚度设置为某个合理的大值，并将阻尼设置为零。下面是一个球体在恢复系数为 1 的平面上弹跳的示例，因此接触前后的能量近似守恒。能量并非完全守恒，因为接触本身是软的，需要几个时间步，并且在这些时间步中的（隐式）变形并非完全能量守恒。但总体效果是，球体弹跳很长时间，其峰值高度没有明显变化，能量围绕初始值波动而不是漂移。

<worldbody>
  <geom type="plane" size="1 1 .1"/>

  <body pos="0 0 1">
    <freejoint/>
    <geom type="sphere" size="0.1" solref="-1000 0"/>
  </body>
</worldbody>