流体力#

对流体动力学进行适当的模拟超出了 MuJoCo 的范畴，并且对于我们旨在促进的应用来说速度太慢。然而，我们提供了两种现象学模型，它们足以模拟飞行和游泳等行为。这些模型是无状态的，因为没有为周围的流体分配额外的状态，但它们能够捕捉到刚体在流体介质中运动的显著特征。

通过将 density 和 viscosity 属性设置为正值，可以启用这两种模型。这些参数对应于介质的密度 \(\rho\) 和粘度 \(\beta\)。

基于惯量的模型仅使用粘度和密度，从物体的等效惯量盒推断几何形状。
基于椭球体的模型更为精细，它使用 geom 的椭球体近似。除了介质的全局粘度和密度外，该模型还为每个相互作用的 geom 提供了 5 个可调参数。

提示

如数值积分部分所述，在存在速度相关力的情况下，隐式积分能显著提高模拟的稳定性。下面描述的两种流体力模型都表现出此特性，因此在使用流体力时，推荐使用 implicit 或 implicitfast 积分器。这两种模型所需的解析导数都已完全实现。

惯量模型#

在此模型中，出于流体动力学的目的，每个物体的形状都被假定为等效惯量盒，该惯量盒也可以被可视化。对于质量为 \(\mathcal{M}\)、惯量矩阵为 \(\mathcal{I}\) 的物体，其等效惯量盒的半尺寸（即半宽、半深和半高）为：

\[\begin{align*} r_x = \sqrt{\frac{3}{2 \mathcal{M}} \left(\mathcal{I}_{yy} + \mathcal{I}_{zz} - \mathcal{I}_{xx} \right)} \\ r_y = \sqrt{\frac{3}{2 \mathcal{M}} \left(\mathcal{I}_{zz} + \mathcal{I}_{xx} - \mathcal{I}_{yy} \right)} \\ r_z = \sqrt{\frac{3}{2 \mathcal{M}} \left(\mathcal{I}_{xx} + \mathcal{I}_{yy} - \mathcal{I}_{zz} \right)} \end{align*} \]

令 \(\mathbf{v}\) 和 \(\boldsymbol{\omega}\) 分别表示物体在物体局部坐标系（与等效惯量盒对齐）中的线速度和角速度。流体施加在固体上的力 \(\mathbf{f}_{\text{inertia}}\) 和扭矩 \(\mathbf{g}_{\text{inertia}}\) 是以下各项的总和：

\[\begin{align*} \mathbf{f}_{\text{inertia}} &= \mathbf{f}_D + \mathbf{f}_V \\ \mathbf{g}_{\text{inertia}} &= \mathbf{g}_D + \mathbf{g}_V \end{align*} \]

此处的下标 \(D\) 和 \(V\) 分别表示二次阻力（Drag）和粘性阻力（Viscous resistance）。

二次阻力项取决于流体的密度 \(\rho\)，与物体速度的平方成正比，并且是高雷诺数下流体力的有效近似。扭矩是通过对旋转产生的力在表面积上积分得到的。力和扭矩的第 \(i\) 个分量可以写为：

\[\begin{aligned} f_{D, i} = \quad &- 2 \rho r_j r_k |v_i| v_i \\ g_{D, i} = \quad &- {1 \over 2} \rho r_i \left(r_j^4 + r_k^4 \right) |\omega_i| \omega_i \\ \end{aligned} \]

粘性阻力项取决于流体的粘度 \(\beta\)，与物体速度成线性关系，并近似于低雷诺数下的流体力。请注意，粘度可以独立于密度使用，以使模拟更具阻尼效果。我们使用低雷诺数下等效球体的公式，其半径为 \(r_{eq} = (r_x + r_y + r_z) / 3\)。在局部物体坐标系中得到的 3D 力和扭矩为：

\[\begin{aligned} f_{V, i} = \quad &- 6 \beta \pi r_{eq} v_i \\ g_{V, i} = \quad &- 8 \beta \pi r_{eq}^3 \omega_i \\ \end{aligned} \]

还可以通过指定一个非零的 wind 来影响这些力，该风速是一个三维向量，在流体动力学计算中会从物体的线速度中减去。

椭球体模型#

../_images/fruitfly.png — 此图中具有飞行能力的黑腹果蝇模型在 Vaxenburg等 [VSM+24] 中有描述。#

在本节中，我们描述并推导了一个无状态模型，该模型基于 geom 形状的椭球体近似，用于计算周围流体施加在运动刚体上的力。与上一节基于惯量的模型相比，该模型可以对不同类型的流体力进行更精细的控制。该模型的动机用例是昆虫飞行，见右图。

摘要#

通过将 fluidshape 属性设置为 ellipsoid，可以为每个 geom 激活该模型，这也会禁用其父物体的基于惯量的模型。fluidcoef 属性中的 5 个数字对应以下语义：

索引	描述	符号	默认值
0	钝体阻力系数	\(C_{D, \text{blunt}}\)	0.5
1	细长体阻力系数	\(C_{D, \text{slender}}\)	0.25
2	角阻力系数	\(C_{D, \text{angular}}\)	1.5
3	库塔升力系数	\(C_K\)	1.0
4	马格努斯升力系数	\(C_M\)	1.0

该模型的元素是对 Andersen等 [APW05b] 的三维推广。流体施加在固体上的力 \(\mathbf{f}_{\text{ellipsoid}}\) 和扭矩 \(\mathbf{g}_{\text{ellipsoid}}\) 是以下各项的总和：

\[\begin{align*} \mathbf{f}_{\text{ellipsoid}} &= \mathbf{f}_A + \mathbf{f}_D + \mathbf{f}_M + \mathbf{f}_K + \mathbf{f}_V \\ \mathbf{g}_{\text{ellipsoid}} &= \mathbf{g}_A + \mathbf{g}_D + \mathbf{g}_V \end{align*} \]

此处的下标 \(A\)、\(D\)、\(M\)、\(K\) 和 \(V\) 分别表示附加质量、粘性阻力、马格努斯升力、库塔升力和粘性阻力。其中 \(D\)、\(M\) 和 \(K\) 项分别由上述的 \(C_D\)、\(C_M\) 和 \(C_K\) 系数进行缩放，粘性阻力与流体粘度 \(\beta\) 成比例，而附加质量项则无法缩放。

符号说明#

我们描述物体在密度为 \(\rho\) 的无粘性、不可压缩的静止流体中的运动。模型中，任意形状的物体被描述为半轴为 \(\mathbf{r} = \{r_x, r_y, r_z\}\) 的等效椭球体。问题在一个与椭球体各边对齐并随之移动的参考系中进行描述。物体的速度为 \(\mathbf{v} = \{v_x, v_y, v_z\}\)，角速度为 \(\boldsymbol{\omega} = \{\omega_x, \omega_y, \omega_z\}\)。我们还将使用：

\[\begin{align*} r_\text{max} &= \max(r_x, r_y, r_z) \\ r_\text{min} &= \min(r_x, r_y, r_z) \\ r_\text{mid} &= r_x + r_y + r_z - r_\text{max} - r_\text{min} \end{align*} \]

雷诺数是流体中惯性力与粘性力之比，定义为 \(Re=u~l/\beta\)，其中 \(\beta\) 是流体的运动粘度，\(u\) 是流动的特征速度（或者通过坐标系变换，是物体的速度），\(l\) 是流动或物体的特征尺寸。

我们将用 \(\Gamma\) 表示环量，它是速度场沿闭合曲线的线积分，即 \(\Gamma = \oint \mathbf{v} \cdot \textrm{d} \mathbf{l}\)。根据斯托克斯定理，\(\Gamma = \int_S \nabla \times \mathbf{v} \cdot \textrm{d}\mathbf{s}\)。在流体动力学符号中，符号 \(\boldsymbol{\omega}\) 通常用于表示涡量，定义为 \(\nabla \times \mathbf{v}\)，而不是角速度。对于刚体运动，涡量是角速度的两倍。

最后，我们使用下标 \(i, j, k\) 来表示对称地适用于 \(x, y, z\) 的方程组。例如，\(a_i = b_j + b_k\) 是以下 3 个方程的简写：

\[\begin{align*} a_x &= b_y + b_z \\ a_y &= b_x + b_z \\ a_z &= b_x + b_y \end{align*} \]

椭球体投影#

我们提出以下结果。

引理

给定一个半轴为 \((r_x, r_y, r_z)\) 且与坐标轴 \((x, y, z)\) 对齐的椭球体，以及一个单位向量 \(\mathbf{u} = (u_x, u_y, u_z)\)，该椭球体在垂直于 \(\mathbf{u}\) 的平面上的投影面积为：

\[A^{\mathrm{proj}}_{\mathbf{u}} = \pi \sqrt{\frac{r_y^4 r_z^4 u_x^2 + r_z^4 r_x^4 u_y^2 + r_x^4 r_y^4 u_z^2}{r_y^2 r_z^2 u_x^2 + r_z^2 r_x^2 u_y^2 + r_x^2 r_y^2 u_z^2}} \]

展开查看推导

引理的推导

椭圆的面积

任何以原点为中心的椭圆都可以用二次型 \(\mathbf{x}^T Q \mathbf{x} = 1\) 来描述，其中 \(Q\) 是一个实对称正定 2x2 矩阵，它定义了椭圆的方向和半轴长度，\(\mathbf{x} = (x, y)\) 是椭圆上的点。椭圆的面积由下式给出：

\[A = \frac{\pi}{\sqrt{\det Q}} . \]

椭球体截面

我们首先计算以原点为中心的椭球体与通过原点且单位法向量为 \(\mathbf{n} = (n_x, n_y, n_z)\) 的平面 \(\Pi_{\mathbf{n}}\) 相交所形成的椭圆的面积。设 \((r_x, r_y, r_z)\) 为椭球体的半轴长度。不失一般性，可以假设椭球体的轴与坐标轴对齐。那么椭球体可以描述为 \(\mathbf{x}^T Q \mathbf{x} = 1\)，其中 \(Q = \textrm{diag}\mathopen{}\left( \left. 1 \middle/ r_x^2 \right., \left. 1 \middle/ r_y^2 \right., \left. 1 \middle/ r_z^2 \right. \right)\mathclose{}\)，\(\mathbf{x} = (x, y, z)\) 是椭球体上的点。

我们接下来将平面 \(\Pi_{\mathbf{n}}\) 与椭球体一起旋转，使得旋转后平面的法线指向 \(z\) 轴方向。这样我们就可以通过将 \(z\) 坐标设为零来得到所需的交线。用 \(\mathbf{\hat{z}}\) 表示沿 \(z\) 轴的单位向量，我们有：

\[\begin{align*} \mathbf{n} \times \mathbf{\hat{z}} &= \sin\theta \, \mathbf{m}, \\ \mathbf{n} \cdot \mathbf{\hat{z}} &= \cos\theta , \end{align*} \]

其中 \(\mathbf{m}\) 是定义旋转轴的单位向量，\(\theta\) 是旋转角度。我们可以重新整理这些式子，得到构建旋转四元数所需的量，即：

\[\begin{align*} \cos\frac{\theta}{2} &= \sqrt{\frac{1+\cos\theta}{2}} &= \sqrt{\frac{1 + \mathbf{n} \cdot \mathbf{\hat{z}}}{2}}, \\ \sin\frac{\theta}{2}\,\mathbf{m} &= \frac{\mathbf{n} \times \mathbf{\hat{z}}}{2\cos\frac{\theta}{2}} &= \frac{\mathbf{n} \times \mathbf{\hat{z}}}{\sqrt{2 (1 + \mathbf{n} \cdot \mathbf{\hat{z}})}} . \end{align*} \]

因此，旋转四元数 \(q = q_r + q_x \mathbf{i} + q_y \mathbf{j} + q_z \mathbf{k}\) 由下式给出：

\[q_r = \sqrt{\frac{1 + n_z}{2}}, \quad q_x = \frac{n_y}{\sqrt{2 \left(1+n_z\right)}}, \quad q_y = \frac{-n_x}{\sqrt{2 \left(1+n_z\right)}}, \quad q_z = 0 . \]

由此，旋转矩阵为：

\[\def\arraystretch{1.33} \begin{align*} R &= \begin{pmatrix} 1 - 2 q_y^2 - 2 q_z^2 & 2 \left(q_x q_y - q_r q_z\right) & 2 \left(q_x q_z + q_r q_y\right) \\ 2 \left(q_x q_y + q_r q_z\right) & 1 - 2 q_x^2 - 2 q_z^2 & 2 \left(q_y q_z - q_r q_x\right) \\ 2 \left(q_x q_z - q_r q_y\right) & 2 \left(q_y q_z + q_r q_x\right) & 1 - 2 q_x^2 - 2 q_y^2 \end{pmatrix} \\ &= \begin{pmatrix} 1 - \left. n_x^2 \middle/ \left( 1+n_z \right) \right. & \left. -n_x n_y \middle/ \left( 1+n_z \right) \right. & -n_x \\ \left. -n_x n_y \middle/ \left( 1+n_z \right) \right. & 1 - \left. n_y^2 \middle/ \left( 1+n_z \right) \right. & -n_y \\ n_x & n_y & 1 - \left. \left( n_x^2 + n_y^2 \right) \middle/ \left( \vphantom{n_x^2} 1+n_z \right) \right. \end{pmatrix}, \end{align*} \]

旋转后的椭球体通过变换后的二次型来描述：

\[\mathbf{x}^T Q' \mathbf{x} = \mathbf{x}^T \left( R^T Q R \right) \mathbf{x} = 1 . \]

根据上面椭圆面积的公式，为了求出 \(z=0\) 处椭圆的面积，我们需要：

\[\begin{align*} Q'_{xx} &= \frac{1}{r_x^2} R_{xx}^2 + \frac{1}{r_y^2} R_{yx}^2 + \frac{1}{r_z^2} R_{zx}^2 , \\ Q'_{yy} &= \frac{1}{r_x^2} R_{xy}^2 + \frac{1}{r_y^2} R_{yy}^2 + \frac{1}{r_z^2} R_{zy}^2 , \\ Q'_{xy} &= \frac{1}{r_x^2} R_{xx} R_{xy} + \frac{1}{r_y^2} R_{yx} R_{yy} + \frac{1}{r_z^2} R_{zx} R_{zy} , \end{align*} \]

所需的面积由下式给出：

\[A^{\cap}_{\mathbf{n}} = \frac{\pi}{\sqrt{\vphantom{Q'^2_{xy}} \det Q'}} = \frac{\pi}{\sqrt{Q'_{xx} Q'_{yy} - Q'^2_{xy}}} = \frac{\pi r_x r_y r_z}{\sqrt{r_x^2 n_x^2 + r_y^2 n_y^2 + r_z^2 n_z^2}}, \]

其中上标 \(\cap\) 表示该面积是与 \(\Pi_{\mathbf{n}}\) *相交*形成的椭圆的面积。

投影椭圆

令 \(\mathbf{u} = (u_x, u_y, u_z)\) 为某个单位向量（在我们的情境中，它是撞击椭球体的流体速度方向），并令 \(\Pi_{\mathbf{u}}\) 为垂直于 \(\mathbf{u}\) 的平面。通常情况下，将椭球体 \(\mathcal{E}\) 投影到 \(\Pi_{\mathbf{u}}\) 上形成的椭圆（记作 \(\mathcal{E}^{\mathrm{proj}}_{\mathbf{u}}\)）与 \(\mathcal{E}\) 与 \(\Pi_{\mathbf{u}}\) 相交形成的椭圆（记作 \(\mathcal{E}^{\cap}_{\mathbf{u}}\)）是不同的。

\(\mathcal{E}^{\mathrm{proj}}_{\mathbf{u}}\) 的一个重要性质是，在 \(\mathcal{E}^{\mathrm{proj}}_{\mathbf{u}}\) 上的每一点，\(\mathbf{u}\) 都与椭球体 \(\mathcal{E}\) 相切。

我们可以将 \(\mathcal{E}\) 视为单位球面 \(\mathcal{S}\) 在拉伸变换 \(T = \mathrm{diag}(r_x, r_y, r_z)\) 下的像。此外，如果 \(\mathbf{\tilde{u}}\) 是与 \(\mathcal{S}\) 相切的向量，则其像 \(\mathbf{u}=T\mathbf{\tilde{u}}=(r_x \tilde{u}_x, r_y \tilde{u}_y, r_z \tilde{u}_z)\) 与该椭球体相切。因此，椭圆 \(\mathcal{E}^{\mathrm{proj}}_{\mathbf{u}}\) 是圆 \(\mathcal{C}^{\cap}_{\mathbf{\tilde{u}}}\) 在变换 \(T\) 下的像，该圆是 \(\mathcal{S}\) 与 \(\Pi_{\mathbf{\tilde{u}}}\) 的交线（对于球体，\(\mathcal{C}^{\cap}\) 和 \(\mathcal{C}^{\mathrm{proj}}\) 是重合的）。

设 \(\mathbf{\tilde{v}}\) 和 \(\mathbf{\tilde{w}}\) 是平面 \(\Pi_{\mathbf{\tilde{u}}}\) 中的一对正交向量，则 \(\mathbf{\tilde{u}} = \mathbf{\tilde{v}} \times \mathbf{\tilde{w}}\)。它们在 \(T\) 下的像分别为 \(\mathbf{v} = (r_x \tilde{v}_x, r_y \tilde{v}_y, r_z \tilde {v}_z)\) 和 \(\mathbf{w} = (r_x \tilde{w}_x, r_y \tilde{w}_y, r_z \tilde {w}_z)\)，它们在 \(\mathcal{E}^{\mathrm{proj}}_{\mathbf{u}}\) 的平面内仍然是正交向量。因此，椭圆 \(\mathcal{E}^{\mathrm{proj}}_{\mathbf{u}}\) 的一个（非单位）法向量由下式给出：

\[\mathbf{N} = \mathbf{v} \times \mathbf{w} = (r_y r_z \tilde{u}_x, r_z r_x \tilde{u}_y, r_x r_y \tilde{u}_z) = \left( \frac{r_y r_z}{r_x} u_x, \frac{r_z r_x}{r_y} u_y, \frac{r_x r_y}{r_z} u_z \right). \]

这表明 \(\mathcal{E}^{\mathrm{proj}}_{\mathbf{u}} = \mathcal{E}^{\cap}_{\mathbf{n}}\)，其中 \(\mathbf{n} = \mathbf{N} / \left\Vert\mathbf{N}\right\Vert\)。其面积由上一节推导的公式给出，从而得到上述结果。

附加质量#

对于在流体中运动的物体，附加质量或虚拟质量衡量的是因物体运动而被移动的流体的惯量。它可以从势流理论中推导出来（也就是说，对于无粘性流也存在）。

根据 Lamb [Lam32] 的第 5 章，由于在流体中从静止产生运动而施加在运动物体上的力 \(\mathbf{f}_{V}\) 和扭矩 \(\mathbf{g}_{V}\) 可以写为：

\[\begin{align*} \mathbf{f}_{A} &= - \frac{\textrm{d}}{\textrm{d} t} \nabla_{\mathbf{v}} \mathcal{T} + \nabla_{\mathbf{v}} \mathcal{T} \times \boldsymbol{\omega} \\ \mathbf{g}_{A} &= - \frac{\textrm{d}}{\textrm{d} t} \nabla_{\boldsymbol{\omega}} \mathcal{T} + \nabla_{\mathbf{v}} \mathcal{T} \times \mathbf{v} + \boldsymbol{\omega} \times \nabla_{\boldsymbol{\omega}} \mathcal{T} \end{align*} \]

其中 \(\mathcal{T}\) 是流体本身的动能。这些力通常被称为附加质量或虚拟质量，因为它们是由于加速物体需要移动或偏转的流体的惯性引起的。实际上，对于以恒定线速度运动的物体，这些力会减为零。我们将物体视为具有三个对称平面，因为在此假设下，动能大大简化，可以写为：

\[2 \mathcal{T} = m_{A, x} v_x^2 + m_{A, y} v_y^2 + m_{A, z} v_z^2 + I_{A, x} \omega_x^2 + I_ {A, y} \omega_y^2 + I_{A, y} \omega_z^2 \]

为方便起见，我们引入附加质量向量 \(\mathbf{m}_A = \{m_{A, x}, m_{A, y}, m_{A, z}\}\) 和附加转动惯量向量 \(\mathbf{I}_A = \{I_{A, x}, I_{A, y}, I_{A, z}\}\)。这些量中的每一个都应估算由于物体在相应方向上的运动而移动的流体的惯量，并且可以从势流理论中推导出一些简单几何形状的这些量。

对于具有三个对称平面的物体，我们可以紧凑地写出由附加惯量引起的力和扭矩：

\[\begin{align*} \mathbf{f}_{A} &= - \mathbf{m}_A \circ \dot{\mathbf{v}} + \left(\mathbf{m}_A \circ \mathbf{v} \right) \times \boldsymbol{\omega} \\ \mathbf{g}_{A} &= - \mathbf{I}_A \circ \dot{\boldsymbol{\omega}} + \left(\mathbf{m}_A \circ \mathbf{v} \right) \times \mathbf{v} + \left(\mathbf{I}_A \circ \boldsymbol{\omega} \right) \times \boldsymbol{\omega} \end{align*} \]

这里 \(\circ\) 表示逐元素乘积，\(\dot{\mathbf{v}}\) 是线加速度，\(\dot{\boldsymbol{\omega}}\) 是角加速度。\(\mathbf{m}_A \circ \mathbf{v}\) 和 \(\mathbf{I}_A \circ \boldsymbol{\omega}\) 分别是虚拟线动量和角动量。

对于一个半轴为 \(\mathbf{r} = \{r_x, r_y, r_z\}\)、体积为 \(V = 4 \pi r_x r_y r_z / 3\) 的椭球体，其虚拟惯性系数由 Tuckerman [Tuc25] 推导。令：

\[\kappa_i = \int_0^\infty \frac{r_i r_j r_k}{\sqrt{(r_i^2 + \lambda)^3 (r_j^2 + \lambda) (r_k^2 + \lambda)}} \textrm{d} \lambda \]

应该注意的是，这些系数是无量纲的（即，如果所有半轴都乘以相同的标量，系数保持不变）。椭球体的虚拟质量为：

\[m_{A, i} = \rho V \frac{\kappa_i}{2 - \kappa_i} \]

虚拟转动惯量为：

\[I_{A, i} = \frac{\rho V}{5} \frac{(r_j^2 - r_k^2)^2 (\kappa_k-\kappa_j)}{2(r_j^2 - r_k^2) + (r_j^2 + r_k^2) (\kappa_j-\kappa_k)} \]

粘性阻力#

阻力作用于抵抗物体相对于周围流动的运动。我们发现粘性力也有助于降低增加了流体动力学项的运动方程的刚度。因此，我们选择保守地估计，选择了可能高估耗散的粘性项近似。

尽管最终是由粘性耗散引起的，但在高雷诺数下，阻力与粘度无关，并与速度的二次方成比例。它可以写为：

\[\begin{align*} \mathbf{f}_\text{D} = - C_D~\rho~ A_D ~ \|\mathbf{v}\|~ \mathbf{v}\\ \mathbf{g}_\text{D} = - C_D \rho~ I_D ~ \|\boldsymbol{\omega}\| ~ \boldsymbol{\omega} \end{align*} \]

其中 \(C_D\) 是阻力系数，\(A_D\) 是参考表面积（例如，垂直于流动方向的投影面积的度量），\(I_D\) 是参考转动惯量。

即使对于简单的形状，\(C_D\)、\(A_D\) 和 \(I_D\) 等项也需要根据具体问题的物理特性和动力学尺度进行调整 [DHD15]。例如，阻力系数 \(C_D\) 通常随着雷诺数的增加而减小，而单一的参考面积 \(A_D\) 可能不足以解释高度不规则或细长物体的表面摩擦阻力。例如，实验拟合来自各种问题，从下落的扑克牌 [APW05a, APW05b, WBD04] 到粒子传输 [BB16, Lot08]。请参阅右侧 cards.xml 模型的屏幕截图。

我们基于两个表面 \(A^\text{proj}_\mathbf{v}\) 和 \(A_\text{max}\) 推导出 \(\mathbf{f}_\text{D}\) 的公式。第一个，\(A^\text{proj}_\mathbf{v}\)，是物体在垂直于速度 \(\mathbf{v}\) 的平面上的圆柱投影。第二个是最大投影表面 \(A_\text{max} = 4 \pi r_{max} r_{min}\)。

\[\mathbf{f}_\text{D} = - \rho~ \big[ C_{D, \text{blunt}} ~ A^\text{proj}_\mathbf{v} ~ + C_{D, \text{slender}}\left(A_\text{max} - A^\text{proj}_\mathbf{v} \right) \big] ~ \|\mathbf{v}\|~ \mathbf{v} \]

\(A^\text{proj}_\mathbf{v}\) 的公式和推导见上文的引理。

我们为角阻力提出了一个类似的模型。对于每个笛卡尔轴，我们考虑物体绕该轴旋转所形成的最大扫掠椭球体的转动惯量。转动惯量的对角线元素为：

\[\mathbf{I}_{D,ii} = \frac{8\pi}{15} ~r_i ~\max(r_j, ~r_k)^4 . \]

给定此参考转动惯量，角阻力矩计算如下：

\[\mathbf{g}_\text{D} = - \rho ~ \boldsymbol{\omega} ~ \Big( \big[ C_{D, \text{angular}} ~ \mathbf{I}_D ~ + C_{D, \text{slender}} \left(\mathbf{I}_\text{max} - \mathbf{I}_D \right) \big] \cdot \boldsymbol{\omega} \Big) \]

此处 \(\mathbf{I}_\text{max}\) 是一个向量，其每个分量都等于 \(\mathbf{I}_D\) 的最大分量。

最后，粘性阻力项，也称为线性阻力，在雷诺数约为或低于 \(O(10)\) 时能很好地近似流体力。这些是根据斯托克斯定律为等效球体计算的 [Lam32, Sto50]：

\[\begin{align*} \mathbf{f}_\text{V} &= - 6 \pi r_D \beta \mathbf{v}\\ \mathbf{g}_\text{V} &= - 8 \pi r_D^3 \beta \boldsymbol{\omega} \end{align*} \]

此处，\(r_D = (r_x + r_y + r_z)/3\) 是等效球体的半径，\(\beta\) 是介质的运动粘度（例如，对于室温空气是 \(1.48~\times 10^{-5}~m^2/s\)，对于水是 \(0.89 \times 10^{-4}~m^2/s\)）。举一个量化的例子，对于室温空气，如果 \(u\cdot l \lesssim 2 \times 10^{-4}~m^2/s\)，斯托克斯定律就变得准确，其中 \(u\) 是速度，\(l\) 是物体的特征长度。

粘性升力#

库塔-儒可夫斯基定理计算了在速度为 u 的均匀流中平移的二维物体的升力 \(L\)，其公式为 \(L = \rho u \Gamma\)。此处，\(\Gamma\) 是围绕物体的环量。在接下来的小节中，我们定义了两种环量的来源以及由此产生的升力。

马格努斯力#

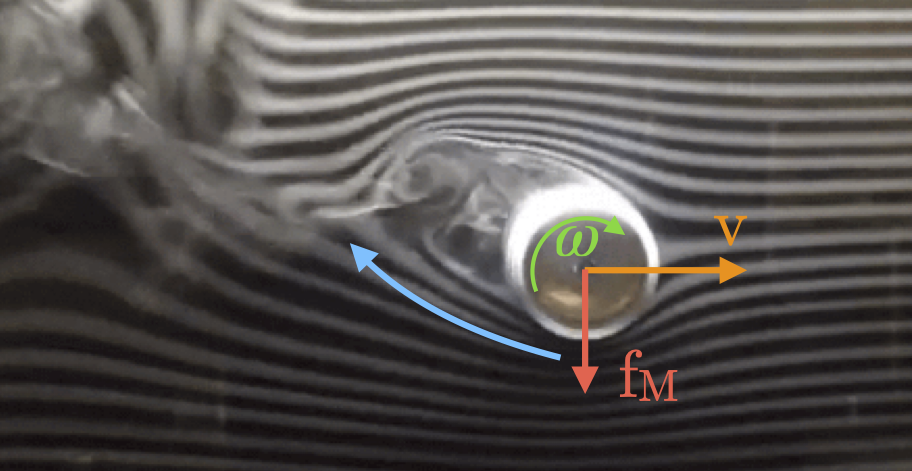
../_images/magnus.png — 旋转圆柱体周围流动的烟流可视化（维基共享资源，CC BY-SA 4.0）。由于粘性，旋转的圆柱体使来流向上偏转，并受到向下的力（红色箭头）。#

马格努斯效应描述了旋转物体在流体中运动的情况。通过粘性效应，旋转的物体会引起周围流体的旋转。这种旋转会使流体绕过物体的轨迹发生偏转（即产生线性加速度），而物体则受到一个大小相等、方向相反的反作用力。对于一个圆柱体，单位长度的马格努斯力可以计算为 \(F_\text{M} / L = \rho v \Gamma\)，其中 \(\Gamma\) 是由旋转引起的流动环量，\(v\) 是物体的速度。我们对任意物体的该力估算如下：

\[\mathbf{f}_{\text{M}} = C_M ~\rho~ V~ \boldsymbol{\omega}\times\mathbf{v} , \]

其中 \(V\) 是物体的体积，\(C_M\) 是力的系数，通常设为 1。

值得举一个例子。为了减少变量数量，假设一个物体只在一个方向上旋转，例如 \(\boldsymbol{\omega} = \{0, 0, \omega_z\}\)，而在另外两个方向上平移，例如 \(\mathbf{v} = \{v_x, v_y, 0\}\)。由于附加质量和马格努斯效应产生的力之和，例如沿 \(x\) 轴方向，为：

\[\frac{f}{\pi \rho r_z} = v_y \omega_z \left(2 r_x \min\{r_x, r_z\} - (r_x + r_z)^2\right) \]

请注意，这两项的符号是相反的。

库塔条件#

驻点是流场中速度为零的位置。对于在流中运动的物体（在与物体一起移动的二维参考系中），有两个驻点：一个在前端，流线在此处分开绕过物体的两侧；另一个在后端，流线在此处重新汇合。一个带有尖锐后缘的运动物体会在周围流体中产生足够强度的环量，以使后驻点保持在后缘上。这就是库塔条件，这是一种流体动力学现象，可以在具有尖锐边角的固体上观察到，例如细长物体或翼型的后缘。

../_images/kutta_cond_plate_dark.svg — 库塔条件示意图。蓝线是流线，两个洋红色点是驻点。连接两个驻点的分界流线用绿色标记。分界流线和物体围成一个区域，该区域内的流动被称为“分离”并在其中再循环。这种环量产生了一个作用在平板上的向上的力。#

对于上图所示的二维流动，由库塔条件引起的环量可以估计为：\(\Gamma_\text{K} = C_K ~ r_x ~ \| \mathbf{v}\| ~ \sin(2\alpha)\)，其中 \(C_K\) 是升力系数，\(\alpha\) 是速度向量与其在表面上的投影之间的夹角。单位长度的升力可以通过库塔-儒可夫斯基定理计算为 \(\mathbf{f}_K / L = \rho \Gamma_\text{K} \times \mathbf{v}\)。

为了将升力方程推广到三维运动，我们考虑法线 \(\mathbf{n}_{s, \mathbf{v}} = \{\frac{r_y r_z}{r_x}v_x, \frac{r_z r_x}{r_y}v_y, \frac{r_x r_x}{r_z}v_z\}\)，该法线对应于物体在垂直于速度的平面上的投影 \(A^\text{proj}_\mathbf{v}\)（见上文引理），以及相应的单位向量 \(\hat{\mathbf{n}}_{s, \mathbf{v}}\)。我们使用这个方向将 \(\mathbf{v}\) 分解为 \(\mathbf{v} = \mathbf{v}_\parallel ~+~ \mathbf{v}_\perp\)，其中 \(\mathbf{v}_\perp = \left(\mathbf{v} \cdot \hat{\mathbf{n}}_{s, \mathbf{v}}\right) \hat{\mathbf{n}}_{s, \mathbf{v}}\)。我们将升力写为：

\[\begin{align*} \mathbf{f}_\text{K} &= \frac{C_K~\rho~ A^\text{proj}_\mathbf{v}}{\|\mathbf{v}\|} \left( \mathbf{v} \times \mathbf{v}_\parallel\right)\times \mathbf{v} \\ &= C_K~\rho~ A^\text{proj}_\mathbf{v} \left(\hat{\mathbf{v}} \cdot \hat{\mathbf{n}}_{s, \mathbf{v}}\right) \left( \hat{\mathbf{n}}_{s, \mathbf{v}} \times \mathbf{v} \right)\times \mathbf{v} \end{align*} \]

此处，\(\hat{\mathbf{v}}\) 是沿 \(\mathbf{v}\) 方向的单位法向量。请注意，\(\hat{\mathbf{n}}_{s, \mathbf{v}}\) 的方向仅在物体半轴不等的平面上才与 \(\hat{\mathbf{v}}\) 不同。因此，例如对于球形物体，\(\hat{\mathbf{n}}_{s, \mathbf{v}} \equiv \hat{\mathbf{v}}\)，根据构造 \(\mathbf{f}_\text{K} = 0\)。

让我们用一个例子来解释这个关系。假设一个物体满足 \(r_x = r_y\) 且 \(r_z \ll r_x\)。注意，向量 \(\hat{\mathbf{n}}_{s, \mathbf{v}} \times \hat{\mathbf{v}}\) 给出了由固体偏转流动引起的环量方向。沿 \(z\) 方向，环量将与 \(\frac{r_y r_z}{r_x}v_x v_y - \frac{r_z r_x}{r_y}v_x v_y = 0\) 成正比（因为 \(r_x = r_y\)）。因此，在固体为钝体的平面上，运动不产生环量。

现在，为简单起见，设 \(v_x = 0\)。在这种情况下，沿 \(y\) 方向的环量也为零，其与 \(\frac{r_y r_z}{r_x}v_x v_z - \frac{r_y r_x}{r_y}v_x v_z\) 成正比。唯一非零的环量分量将沿 \(x\) 方向，并与 \(\left(\frac{r_x r_z}{r_y} - \frac{r_x r_y}{r_z}\right) v_y v_z \approx \frac{r_x^2}{r_z} v_y v_z\) 成正比。

我们将有 \(\mathbf{v}_\parallel = \{v_x, 0, v_z\}\) 和 \(\Gamma \propto \{r_z v_y v_z, ~ 0,~ - r_x v_x v_y \} / \|\mathbf{v}\|\)。在固体为钝体的平面上，运动不产生环量，而在另外两个平面上，环量为 \(\Gamma \propto r_\Gamma ~ \|\mathbf{v}\|~ \sin(2 \alpha) ~ = ~2 r_\Gamma ~\|\mathbf{v}\| ~\sin(\alpha)~\cos(\alpha)\)，其中 \(\alpha\) 是速度与它在该平面上的投影之间的夹角（例如，在垂直于 \(x\) 的平面上，我们有 \(\sin(\alpha) = v_y/\|\mathbf{v}\|\) 和 \(\cos(\alpha) = v_z/\|\mathbf{v}\|\)），\(r_\Gamma\) 是该平面上的升力面（例如，对于垂直于 \(x\) 的平面是 \(r_z\)）。此外，环量的方向由叉积给出（因为固体边界将入射流速“旋转”向其在物体上的投影）。

致谢#

本节中模型的设计与实现由 Guido Novati 完成。

参考文献#

[APW05a]

A Andersen, U Pesavento, and Z Jane Wang. Unsteady aerodynamics of fluttering and tumbling plates. Journal of Fluid Mechanics, 541:65–90, 2005.

[APW05b] (1,2)

Anders Andersen, Umberto Pesavento, and Z Jane Wang. Analysis of transitions between fluttering, tumbling and steady descent of falling cards. Journal of Fluid Mechanics, 541:91–104, 2005.

[BB16]

Gholamhossein Bagheri and Costanza Bonadonna. On the drag of freely falling non-spherical particles. Powder Technology, 301:526–544, 2016.

[DHD15]

Zhipeng Duan, Boshu He, and Yuanyuan Duan. Sphere drag and heat transfer. Scientific reports, 5(1):1–7, 2015.

[Lam32] (1,2)

Horace Lamb. Hydrodynamics. Sixth edition. Cambridge University Press, 1932.

[Lot08]

E Loth. Drag of non-spherical solid particles of regular and irregular shape. Powder Technology, 182(3):342–353, 2008.

[Sto50]

GG Stokes. On the effect of internal friction of fluids on the motion of pendulums. Trans. Camb. phi1. S0c, 9(8):106, 1850.

[Tuc25]

LB Tuckerman. Inertia factors of ellipsoids for use in airship design. US Government Printing Office, 1925.

[VSM+24]

Roman Vaxenburg, Igor Siwanowicz, Josh Merel, Alice A Robie, Carmen Morrow, Guido Novati, Zinovia Stefanidi, Gwyneth M Card, Michael B Reiser, Matthew M Botvinick, Kristin M Branson, Yuval Tassa, and Srinivas C Turaga. Whole-body simulation of realistic fruit fly locomotion with deep reinforcement learning. bioRxiv, 2024. doi:10.1101/2024.03.11.584515.

[WBD04]

Z Jane Wang, James M Birch, and Michael H Dickinson. Unsteady forces and flows in low reynolds number hovering flight: two-dimensional computations vs robotic wing experiments. Journal of Experimental Biology, 207(3):449–460, 2004.